Klammerausdrücke addieren bzw. subtrahieren

Kommen in einer Gleichung Klammern vor, so müssen diese zuerst aufgelöst werden. Anschließend wird die Gleichung durch Äquivalenzumformungen so lange vereinfacht, bis die Unbekannte (Variable) allein auf einer Seite steht.

Lösen von Gleichungen mit Klammerausdrücken, die zu addieren bzw. zu subtrahieren sind

Eine ausführliche Anleitung zum Addieren und Subtrahieren von Klammertermen finden Sie im Kapitel Addition und Subtraktion von Klammertermen .

Eine Zusammenfassung dafür haben wir Ihnen für dieses Kapitel zusammengestellt:

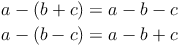
Rechenregel 1: Steht vor einem Klammerausdruck ein +, so kann man die Klammer einfach weglassen:

\begin{align} a + (b + c) & = a + b + c \\ a + (b - c) & = a + b - c \end{align}

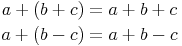
Rechenregel 2: Steht ein - vor der Klammer, so kann man die Klammer nur dann weglassen, wenn man die Rechenzeichen in der Klammer umdreht:

\begin{align} a - (b + c) & = a - b - c \\ a - (b - c) & = a - b + c \end{align}

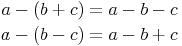
Beispiel: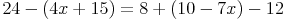

24 - (4x + 15) = 8 + (10 - 7x) - 12

Schritt 1: Klammern weglassen (die Regeln dazu sehen Sie weiter oben)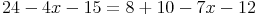

24 - 4x - 15 = 8 + 10 - 7x - 12

Eine ausführliche Anleitung für die folgenden Schritte 2 bis 5 finden Sie im Kapitel Lösen von Gleichungen mit längeren Angaben .

Schritt 2: Auf beiden Seiten des =Zeichens sowohl Zahlen als auch Variable addieren bzw. subtrahieren: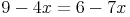

9 - 4x = 6 - 7x

Schritt 3: Wir bringen die Variable mit dem geringeren Wert auf die andere Seite (in unserem Fall -7x): Das Gegenteil von - 7x ist + 7x: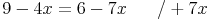

9 - 4x = 6 - 7x \qquad / + 7x

9 - 4x + 7x = 6

Schritt 4: Wir bringen die Zahlen auf die andere Seite: Das Gegenteil von +9 ist -9: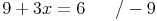

9 + 3x = 6 \qquad / -9

+3x = 6 - 9

+3x = -3

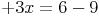
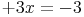
Schritt 5: Um die Variable alleine auf der linken Seite stehen zu haben, müssen wir nun noch dividieren. Wir haben das Ergebnis für 3x, wollen aber das Ergebnis nur für x, also dividieren wir durch 3: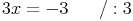

3x = -3 \qquad / :3

x = -3 : 3

\underline{x = -1}

Lösen von Gleichungen mit Klammerausdrücken, die zu addieren bzw. zu subtrahieren sind:

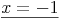
Kommen in einer Gleichung Klammern vor, so müssen diese zuerst aufgelöst werden:

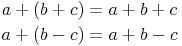
\begin{align} a + (b + c) & = a + b + c \\ a + (b - c) & = a + b - c \end{align}

\begin{align} a - (b + c) & = a - b - c \\ a - (b - c) & = a - b + c \end{align}

Anschließend wird die Gleichung durch Äquivalenzumformungen so lange vereinfacht, bis die Unbekannte (Variable) allein auf einer Seite steht.
Kommentar #42144 von Eyy Kwein 19.01.19 19:09
Eyy Kwein

Wow. Gibt es auch eine Möglichkeit, das hier zu machen:

(4a²+8ab+4b²)-(4a²-8ab+4b²)

?

Kommentar verfassen