Zusammenhang zwischen ggT und kgV

Das Produkt von ggT und kgV zweier Zahlen ist gleich dem Produkt der beiden Zahlen.

Der Zusammenhang zwischen dem ggT und dem kgV

Wir versuchen, einen Zusammenhang zwischen dem größten gemeinsamen Teiler (ggT) und dem kleinsten gemeinsamen Vielfachen (kgV) zweier Zahlen anhand von konkreten Beispielen herauszufinden.

Beispiel 1: Die Zahlen 8 und 12

\begin{align} & kgV (8, 12) = 24 \\ & ggT (8, 12) = 4 \\ & kgV \cdot ggT = 24 \cdot 4 = 96 \\ & 8 \cdot 12 = 96 \\ \end{align}

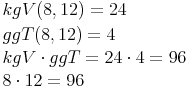
Beispiel 2: Die Zahlen 6 und 15

\begin{align} & kgV (6, 15) = 30 \\ & ggT (6, 15) = 3 \\ & kgV \cdot ggT = 30 \cdot 3 = 90 \\ & 6 \cdot 15 = 90 \\ \end{align}

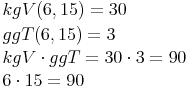
Beispiel 3: Die Zahlen 16 und 20

\begin{align} & kgV (16, 20) = 80 \\ & ggT (16, 20) = 4 \\ & kgV \cdot ggT = 80 \cdot 4 = 320 \\ & 16 \cdot 20 = 320 \\ \end{align}

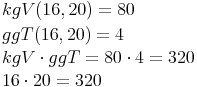
Multipliziert man den ggT und das kgV zweier Zahlen miteinander, so ergibt dies dasselbe Ergebnis wie wenn man die beiden Zahlen miteinander multipliziert.

Zusammenhang zwischen dem ggT und dem kgV

Das Produkt von ggT und kgV zweier Zahlen ist gleich dem Produkt der beiden Zahlen.
Kommentar #9316 von Math hater ;) 15.10.14 22:40
Math hater ;)

SEHR GUT erklärt alles supi :D

Kommentar #40112 von Cool 14.09.17 18:25
Cool

Ich Checks irgendwie nicht :P

Kommentar verfassen