Quadrieren von reinen Zehner-, Hunderter, Tausenderzahlen, ...
Beispiel 1:Quadrieren Sie die Zahlen 10, 100, 1000 und 10000 und achten Sie dabei auf die Anzahl der Nullen der Grundzahl und des Ergebnisses:
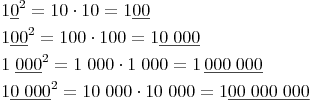
Quadrieren Sie die Zahlen 30, 300, 3000 und 30000 und achten Sie dabei auf die Anzahl der Nullen der Grundzahl und des Ergebnisses:
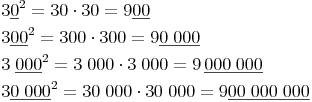
In beiden Beispielen können wir erkennen, dass sich die Anzahl der Nullen der Grundzahl beim Quadrieren verdoppelt.
Es reicht also, die erste Ziffer der Grundzahl zu Quadrieren und danach die Anzahl der Nullen der Grundzahl doppelt anzuhängen.
Durch die vielen Nullen können sehr große Zahlen unleserlich werden. Achten Sie daher auf die Tausendertrennungen (im deutschsprachigen Raum sind Leerräume üblich).
Quadrieren von reinen Zehner-, Hunderter-, Tausenderzahlen, ...
Multiplizieren Sie die erste Ziffer mit sich selbst. Dann verdoppeln Sie die Anzahl der Nullen und hänge diese an.
z.B.: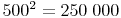
Multiplizieren Sie die erste Ziffer mit sich selbst. Dann verdoppeln Sie die Anzahl der Nullen und hänge diese an.
z.B.:
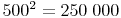
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar