Quadrieren von negativen Zahlen
Beispiel:
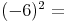
Quadrieren bedeutet, die Zahl mit sich selbst zu multiplizieren:
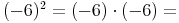
Multiplizieren von zwei negativen ganzen Zahlen:
Multipliziert man zwei negative ganze Zahlen miteinander, so ist das Ergebnis positiv.
Multipliziert man zwei negative ganze Zahlen miteinander, so ist das Ergebnis positiv.
Weitere Infos: Multiplizieren von zwei negativen ganzen Zahlen
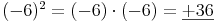
Quadrieren von negativen Zahlen:
Quadrate von negativen ganzen Zahlen sind immer positiv, da die Multiplikation einer negativen Zahl mit einer weiteren negativen Zahl immer eine positive Zahl ergibt.
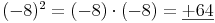
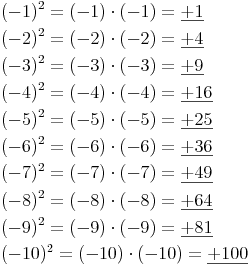
Beispiele:Quadrate von negativen ganzen Zahlen sind immer positiv, da die Multiplikation einer negativen Zahl mit einer weiteren negativen Zahl immer eine positive Zahl ergibt.
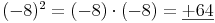
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Rainer
wie erklärt sich die Ungleichung:( -3)² = 3²
d.h. -3=+3 ?
Andi
Beide Seiten wurzeln
finn
das bedeutet also auch, dass (-3)³=(-3)*(-3)*(-3)=(-9) ist wegen der Vorzeichenregel. und das lässt sich weiter übertragen, dass bei ungeraden hoch zahlen immer ein negatives ergebniss herauskommt und bei gersden immer positive... ist das so richtig?
Jona
Bei der Aufgabe -4^2-(-4)^2 ist die Musterlösung -32. Wann ist ein „-“ als Vorzeichen und wann als Rechenzeichen zu erkennen? Meine Lösung wäre „0“ gewesen. (16-16)