Addieren mit rationalen Zahlen

Hier gelten dieselben Rechenregeln und Gesetzmäßigkeiten wie beim Addieren mit Brüchen und beim Addieren mit ganzen Zahlen.

Addieren mit rationalen Zahlen

Beim Addieren mit rationalen Zahlen gelten die selben Rechenregeln und Gesetzmäßigkeiten wie beim Addieren mit Brüchen und beim Addieren mit ganzen Zahlen.

Kombiniert man die Rechenregeln dieser beiden Zahlenmengen, so ergeben sich die Rechenregeln zum Addieren mit rationalen Zahlen.

Beispiel:

\left( +\frac{2}{3} \right) + \left( -1\frac{3}{4} \right)=

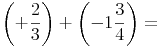
1. Schritt: Auf gemeinsamen Nenner bringen

Der kleinste gemeinsame Nenner unseres Beispiels wäre 12.

Um vom Nenner 3 auf 12 zu kommen, muss der Bruch mit 4 erweitert werden:

\left( +\frac{2}{3} \right) \stackrel{\mathrm{\cdot 4}}= \left( +\frac{8}{12} \right)

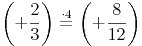
Um vom Nenner 4 auf 12 zu kommen, muss der Bruch mit 3 erweitert werden:

\left( -1\frac{3}{4} \right) \stackrel{\mathrm{\cdot 3}}= \left( -1\frac{9}{12} \right)

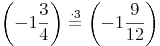
Zusammenfassung:

\left( +\frac{2}{3} \right) + \left( -1\frac{3}{4} \right) = \left( +\frac{8}{12} \right) + \left( -1\frac{9}{12} \right)=

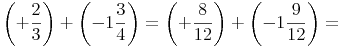
2. Schritt: Klammern auflösen

Die beiden Rechenzeichen + und - nebeneinander ergeben nun ein -.

Zusammenfassung:

\left( +\frac{2}{3} \right) + \left( -1\frac{3}{4} \right) = \left( +\frac{8}{12} \right) + \left( -1\frac{9}{12} \right)= +\frac{8}{12} - 1\frac{9}{12} =

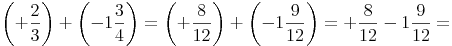
3. Schritt: Die gemischte Zahl in einen unechten Bruch umwandeln

1 = \frac{12}{12}\qquad -->\qquad 1\frac{9}{12} = \frac{12}{12} + \frac{9}{12} = \frac{21}{12}
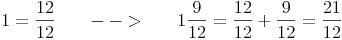
Gemischte Zahlen in unechte Brüche umwandeln

Zusammenfassung:

\left( +\frac{2}{3} \right) + \left( -1\frac{3}{4} \right) = \left( +\frac{8}{12} \right) + \left( -1\frac{9}{12} \right)= +\frac{8}{12} - 1\frac{9}{12} = +\frac{8}{12} - \frac{21}{12} =

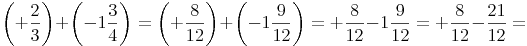
4. Schritt: Berechnen

Addieren bzw. subtrahieren der Zähler: +8 - 21 = -13

Zusammenfassung:

\left( +\frac{2}{3} \right) + \left( -1\frac{3}{4} \right) = \left( +\frac{8}{12} \right) + \left( -1\frac{9}{12} \right)= +\frac{8}{12} - 1\frac{9}{12} = +\frac{8}{12} - \frac{21}{12} = -\frac{13}{12}

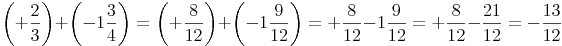
5. Schritt: Ganze herausheben

1 = \frac{12}{12}\qquad -->\qquad -\frac{13}{12} = -1\frac{1}{12}

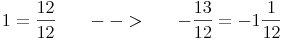
Zusammenfassung:

\begin{align} & \left( +\frac{2}{3} \right) + \left( -1\frac{3}{4} \right) = \left( +\frac{8}{12} \right) + \left( -1\frac{9}{12} \right)= \\ & = +\frac{8}{12} - 1\frac{9}{12} = +\frac{8}{12} - \frac{21}{12} = -\frac{13}{12} = -1\frac{1}{12} \end{align}

Addieren mit rationalen Zahlen:

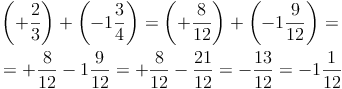
Hier gelten dieselben Rechenregeln und Gesetzmäßigkeiten wie beim Addieren mit Brüchen und beim Addieren mit ganzen Zahlen.
Kommentar #40380 von lisa 11.11.17 17:58
lisa

es war sehr hilfreich dankeschön!!!!

Kommentar #46490 von Konstantin Prinz 31.10.21 11:56
Konstantin Prinz

kein bisschen hilfreich, sorry

Kommentar verfassen