Multiplizieren mit rationalen Zahlen

Hier gelten dieselben Rechenregeln und Gesetzmäßigkeiten wie beim Multiplizieren mit Brüchen und beim Multiplizieren mit ganzen Zahlen.

Multiplizieren mit rationalen Zahlen

Beim Multiplizieren mit rationalen Zahlen gelten die selben Rechenregeln und Gesetzmäßigkeiten wie beim Multiplizieren mit Brüchen und beim Multiplizieren mit ganzen Zahlen.

Kombiniert man die Rechenregeln dieser beiden Zahlenmengen, so ergeben sich die Rechenregeln zum Multiplizieren mit rationalen Zahlen.

Beispiel:

\left( -\frac{3}{5} \right) \cdot \left( +1\frac{1}{3} \right)=

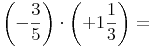
1. Schritt: Umwandeln der gemischten Zahl in einen unechten Bruch

Mehr dazu: Gemischte Zahlen in unechte Brüche umwandeln

\left( -\frac{3}{5} \right) \cdot \left( +1\frac{1}{3} \right) = \left( -\frac{3}{5} \right) \cdot \left( +\frac{4}{3} \right)

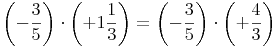
2. Schritt: Vorzeichen des Ergebnisses bestimmen

Mehr dazu: Mutiplizieren von ganzen Zahlen

Haben beide Faktoren das gleiche Vorzeichen, so ist das Produkt positiv.

Haben beide Faktoren unterschiedliche Vorzeichen, so ist das Produkt negativ.

In unserem Beispiel ist das Vorzeichen nun also negativ:

\left( -\frac{3}{5} \right) \cdot \left( +1\frac{1}{3} \right) = \left( -\frac{3}{5} \right) \cdot \left( +\frac{4}{3} \right) = -

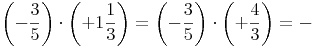
3. Schritt: Gemeinsamer Bruchstrich

Da nun bereits klar ist, dass das Ergebnis negativ ist, schreiben wir die beiden Brüche auf einem Bruchstrich an.

\left( -\frac{3}{5} \right) \cdot \left( +1\frac{1}{3} \right) = \left( -\frac{3}{5} \right) \cdot \left( +\frac{4}{3} \right) = -\frac{3 \cdot 4}{5 \cdot 3}

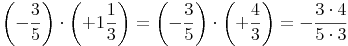
4. Schritt: Kürzen

Mehr dazu: Kürzen von Brüchen

Da sowohl im Zähler als auch im Nenner eine 3 steht, können wir diese beiden Zahlen kürzen, der Wert des Ergebnisses ändert sich dadurch nicht.

\left( -\frac{3}{5} \right) \cdot \left( +1\frac{1}{3} \right) = \left( -\frac{3}{5} \right) \cdot \left( +\frac{4}{3} \right) = -\frac{3 \cdot 4}{5 \cdot 3} \stackrel{\mathrm{: 3}}= -\frac{1 \cdot 4}{5 \cdot 1}

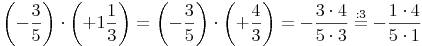
5. Schritt: Multiplizieren

Mehr dazu: Multiplizieren eines Bruches mit einem weiteren Bruch

Zähler mal Zähler bzw. Nenner mal Nenner!

\left( -\frac{3}{5} \right) \cdot \left( +1\frac{1}{3} \right) = \left( -\frac{3}{5} \right) \cdot \left( +\frac{4}{3} \right) = -\frac{3 \cdot 4}{5 \cdot 3} \stackrel{\mathrm{: 3}}= -\frac{1 \cdot 4}{5 \cdot 1} = -\frac{4}{5}

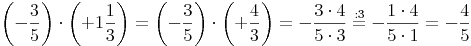
6. Schritt: Ganze herausheben

Mehr dazu: Unechte Brüche in gemischte Zahlen umwandeln

Da hier der Zähler kleiner als der Nenner ist, handelt es sich um einen echten Bruch. Hier können also keine Ganzen mehr herausgehoben werden.

Multiplizieren mit rationalen Zahlen:

Hier gelten dieselben Rechenregeln und Gesetzmäßigkeiten wie beim Multiplizieren mit Brüchen und beim Multiplizieren mit ganzen Zahlen.
Kommentar #41988 von Sebastian.Lehner 09.12.18 15:43
Sebastian.Lehner

Mir hat eure Seite:"Multiplitzieren mit rationalen Zahlen" nicht geholfen, weil man nur Bruchrechnungen gefunden hat und keine Punktrechnungen! Ich hoffe es ändert sic und man kann sich dann richtige Rechnungen heraussuchen.
Schönen Tag wünsche ich noch.

Kommentar verfassen