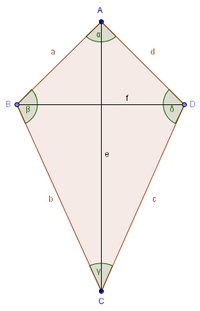
Das Deltoid (Drachenviereck)
Ein Deltoid ist ein Viereck, bei dem zwei Paar Nachbarseiten gleich lang sind.
Parallelogramm - BeschriftungDie Beschriftung der Eckpunkte erfolgt mit Großbuchstaben und gegen den Uhrzeigersinn: A, B, C, D
Die Beschriftung der Seiten erfolgt mit Kleinbuchstaben und gegen den Uhrzeigersinn: a, b, c, d
Die Beschriftung der Winkel erfolgt mit griechischen Kleinbuchstaben, passend zum Eckpunkt:
![\begin{align}
& \text{ Winkel } {\alpha} \text{ [sprich: Alpha] beim Eckpunkt A} \\
& \text{ Winkel } {\beta} \text{ [sprich: Beta] beim Eckpunkt B} \\
& \text{ Winkel } {\gamma} \text{ [sprich: Gamma] beim Eckpunkt C} \\
& \text{ Winkel } {\delta} \text{ [sprich: Delta] beim Eckpunkt D }
\end{align}](/media/formulas/a98c53dc78f57e61a107305319f2751d.png "\begin{align}
& \text{ Winkel } {\alpha} \text{ [sprich: Alpha] beim Eckpunkt A} \\
& \text{ Winkel } {\beta} \text{ [sprich: Beta] beim Eckpunkt B} \\
& \text{ Winkel } {\gamma} \text{ [sprich: Gamma] beim Eckpunkt C} \\
& \text{ Winkel } {\delta} \text{ [sprich: Delta] beim Eckpunkt D }
\end{align}")
In jedem Deltoid gilt: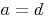 
, 
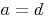sowie 
, sowie
Die Beschriftung der Diagonalen erfolgt mit Kleinbuchstaben: e, f
Die Digonale e verbindet die Eckpunkte A und C
Die Diagonale f verbindet die Eckpunkte B und D
Die Diagonalen stehen normal aufeinander, die Diagonale e halbiert die Diagonale f.
In einem Deltoid:
- stehen die Diagonalen normal aufeinander:
- ist die Diagonale e eine Symmetriegerade
- sind jene Winkel, die der Symmetriegeraden gegenüberliegen gleich groß:
- halbiert die Symmetriegerade (Diagonale e) die andere Diagonale (f).
- stehen die Diagonalen normal aufeinander:
- ist die Diagonale e eine Symmetriegerade
- sind jene Winkel, die der Symmetriegeraden gegenüberliegen gleich groß:
- halbiert die Symmetriegerade (Diagonale e) die andere Diagonale (f).
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Andreas Palmetzhofer
Ich finde es Blöd weil keine Formeln Angezeigt werden!
Anonymus 3000
Super Seite!!! : )
NONI
DAS WICHTIGSTE STEHT DA
EINFACHER KANN MAN MATHE NICHT ERKLÄREN
DANKE
NONI
NUR DIE BESCHRIFTUNG IST SCHWER ZU LESEN
ich
Das hat mir wirklich sehr geholfen
Dino
Sehr gut
Esti
Beim Deltoid stehen keine Formeln, aber bei den anderen vierecken schon
Lauch Gurkenbaum
Formel für Fläche ist übrigens (e×f):2
Noah
Es wäre gut wenn man eine Rechnung fragen kann