Winkel

In einem Deltoid beträgt die Winkelsumme 360°. Die beiden gegenüberliegenden Winkel Beta und Delta sind gleich groß.

Die Winkel des Deltoids (Drachenviercks)

In einem Deltoid (Drachenviereck) beträgt die Winkelsumme so wie in jedem anderen Viereck 360°.

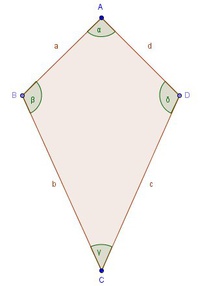
Durch die Symmetrieachse durch die gegenüberliegenden Eckpunkte A und C müssen die gegenüberliegenden Winkel in den Eckpunkten B und D gleich groß sein:
\beta = \delta

Winkelberechnung in einem Deltoid (Drachenviereck)

Beispiel:

geg.: Deltoid: 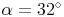\alpha = 32^\circ , \beta = 130^\circ

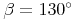
Berechnen Sie die Größen der beiden anderen Winkel!

\alpha + \beta + \gamma + \delta = 360^\circ

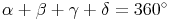
Da die beiden Winkel 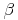\beta (Beta) und 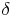\delta (Delta) gleich groß sind, können wir die obige Formel umformen: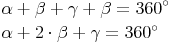

\begin{align} & \alpha + \beta + \gamma+ \beta= 360^\circ \\ & \alpha + 2 \cdot \beta + \gamma = 360^\circ \\ \end{align}

Wir setzen die Angabe in unsere Formel ein und formen um:

\begin{align} & 32^\circ + 2 \cdot 130^\circ + \gamma= 360^\circ \\ & 32^\circ + 260^\circ + \gamma = 360^\circ \\ & 292^\circ + \gamma= 360^\circ \qquad / - 292^\circ \\ & \gamma= 360^\circ - 292^\circ \\ & \gamma= 68^\circ \\ \end{align}

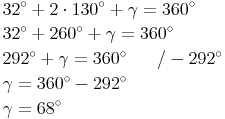
Da Delta genauso groß ist wie Beta, gilt: 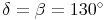\delta = \beta = 130^\circ

Die Winkel in einem Deltoid (Drachenviereck):

In einem Deltoid beträgt die Winkelsumme so wie in jedem anderen Viereck 360°.

Die beiden gegenüberliegenden Winkel Beta und Delta sind gleich groß:
\beta = \delta
Kommentar #40108 von Michael 14.09.17 07:03
Michael

Wenn ich die Seite b und c habe und die Diagonale f, sowie den Winkel Gamma, kann ich dann die anderen Winkel ausrechnen? Zur Vereinfachung könnten b, c und e gleich lang sein.

Kommentar verfassen