Der Umkreis des Deltoids
Wir versuchen hier anhand eines konkreten Beispiels herauszufinden, ob man einem Deltoid einen Umkreis zeichnen kann oder nicht.
Um den Umkreis zu erhalten, müssen die Seitensymmetralen des Deltoids konstruiert werden.
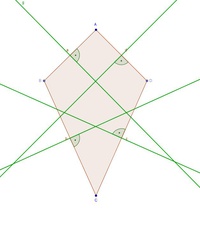
Konstruiert man die Seitensymmetralen aller vier Seiten des Deltoids, so erkennt man, dass sich diese nicht genau in 1 Punkt schneiden.
Es gibt also keinen Punkt, der von allen 4 Eckpunkten gleich weit entfernt ist - es gibt keinen Umkreismittelpunkt.
Deshalb ist es auch nicht möglich, einen Umkreis zu konstruieren.
Ausnahme:
Sind die beiden gleich großen Winkel 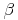 (Beta) und
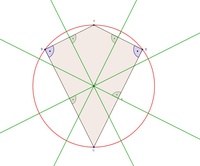
(Beta) und 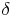 (Delta) rechte Winkel, so lässt sich hingegen doch ein Umkreis konstruieren.
(Delta) rechte Winkel, so lässt sich hingegen doch ein Umkreis konstruieren.
Die Symmetrieachse durch die Eckpunkte A und C teilt das Deltoid dadurch in 2 rechtwinkelige Dreiecke.
Ein allgemeines Deltoid besitzt also keinen Umkreis, es sei denn, die Winkel Beta und Delta sind rechte Winkel.
Ein Deltoid besitzt keinen Umkreis, außer wenn die Winkel Beta und Delta rechte Winkel sind.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Uwe
Dank Ihrer Seite konnte ich meiner Tochter ihre Mathe-Hausübung erklären. Danke! :-)