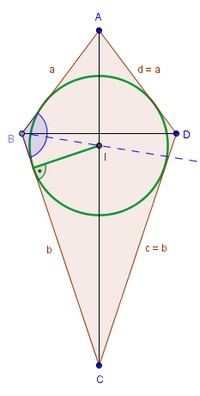
Der Inkreis des Deltoids
Man kann jedem Deltoid einen Kreis einschreiben, der alle 4 Seitenflächen berührt (= Inkreis)
Um den Inkreis zu erhalten, müssen die Winkelsymmetralen des Deltoids konstruiert werden.
Der Schnittpunkt der Winkelsymmetralen ist der Mittelpunkt (I) des Inkreises. Er ist also von allen 4 Seiten gleich weit entfernt.
Da die Diagonale e (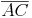 ) schon Winkelsymmetrale ist, braucht man nur noch eine weitere Winkelsymmetrale zu zeichnen (z.B.
) schon Winkelsymmetrale ist, braucht man nur noch eine weitere Winkelsymmetrale zu zeichnen (z.B. 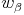 ).
).
Die Winkelsymmetrale halbiert einen Winkel.
Der Inkreismittelpunkt I ist der Schnittpunkt der Winkelsymmetralen (der Diagonale e mit der Winkelsymmetrale 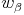 oder
oder 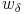 ) des Deltoids.
) des Deltoids.
Der Radius ist der Normalabstand des Inkreismittelpunktes I zu einer beliebigen Seite.
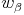 oder
oder 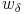 ) des Deltoids.
) des Deltoids.Der Radius ist der Normalabstand des Inkreismittelpunktes I zu einer beliebigen Seite.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
LOL
echt gut
Matteo Freddio
Hab dacht das geht nich
Marc
Ich verstehe nicht wie man den Schnittpunkt zeichnen soll ...Bitte hilft mir...
isabel
wie konstruiere ich den Inkreisradius mit dem Zirkel?
Steinhofer Alexander
Wie berechne ich die Fläche des Inkreises bei einem Deltoid?