Rechteck: Die Länge berechnen

Hier gibt es eine Formel zur Berechnung der Länge l eines Rechtecks, wenn der Umfang u und die Breite b bekannt sind.

Die Länge eines Rechteckes berechnen, wenn der Umfang und die Breite gegeben sind

Beispiel:
Ein Rechteck ist 7cm breit und hat einen Umfang von 38 cm. Berechnen Sie die Länge des Rechtecks!

Herleitung der Formel:
Aus dem vorherigen Kapitel wissen wir bereits, dass der Umfang eines Rechteckes die Summe der vier Seiten ist. Da ein Rechteck jeweils 2 gleich lange Seiten (nämlich Länge und Breite) hat, gilt:

Umfang des Rechtecks:

u = l + b + l + b
u = 2 \cdot l + 2 \cdot b

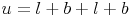
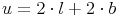
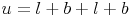
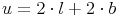
Nachdem wir Umfang und Breite des Rechtecks kennen, die Länge allerdings nicht, formen wir unsere Formel so lange um, bis die Länge allein auf einer Seite steht:

\begin{align} & u = 2 \cdot l + 2 \cdot b\qquad / - 2 \cdot b \\ & u - 2 \cdot b = 2 \cdot l\qquad / : 2 \\ & \frac{u - 2 \cdot b}{2} = l \\ \end{align}

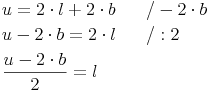
Beispiel (Forts.):

\begin{align} & l = \frac{u - 2 \cdot b}{2} \\ & l = \frac{38 - 2 \cdot 7}{2} \\ & l = \frac{38 - 14}{2} \\ & l = \frac{24}{2} \\ & l = 12\ cm \\ \end{align}

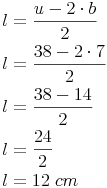
Probe: Wir setzen in die Umfangsformel ein

\begin{align} & u = 2 \cdot l + 2 \cdot b \\ & 38 = 2 \cdot 12 + 2\cdot 7 \\ & 38 = 24 + 14 \\ & 38 = 38 \\ \end{align}

Antwort:

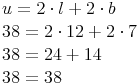
Die Länge des Rechtecks beträgt 12 cm!

Berechnung der Länge eines Rechtecks, wenn der Umfang und die Breite gegeben sind

l = \frac{u - 2 \cdot b}{2}

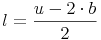
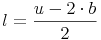
Länge = ( Umfang - 2 Mal Breite) : 2
Kommentar #41144 von reffl 22.05.18 10:51
reffl

ne garnicht meinte wie ich die seite b kriege wenn ich a und die diagonale hab aber egal

Kommentar verfassen