Verhältnisgleichungen
Kennt man in der Mathematik eine Größe nicht, so verwendet man eine Variable, um diese Größe anzuschreiben. Häufig wird dabei die Variable x verwendet.
Von einem Verhältnis spricht man in der Mathematik dann, wenn mehrere Größen in Beziehung zueinander gebracht (miteinander verglichen) werden.
Beispiel:
Ein Dreieck hat einen Umfang von 36 cm. Die Seiten a, b und c dieses Dreiecks verhalten sich wie 2 : 3 : 4. Berechnen Sie die Seitenlängen des Dreiecks!
Wir schreiben als Verhältnis: 
Anleitung:
Die Seite a entspricht 2 Teilen: a = 2x
Die Seite b entspricht 3 Teilen: b = 3x
Die Seite c entspricht 4 Teilen: c = 4x
Die Umfangsformel des Dreiecks lautet: 
Wir setzen nun in diese Formel ein: 
Zusammenfassen der Variablen: 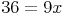
Dividieren: 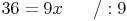
Endergebnis: 
Seite a: 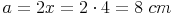
Seite b: 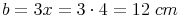
Seite c: 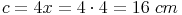
Antwort: Die Seite a des Dreiecks ist 8cm lang, die Seite b 12cm und die Seite c 16 cm.
Zuerst werden die unbekannten Größen als Verhältnis angeschrieben:
z.B.:
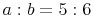
Daraus kann man nun die gesuchten Größen mit Variablen (z.B. x) ausdrücken:
 und
und 
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Michaela
Ich versteh das ganze geschriebene nicht das ist nicht deutlich erklärt