Das Assoziativgesetz beim Dividieren mit natürlichen Zahlen
Anhand eines einfachen Beispieles wollen wir herausfinden, ob die Reihenfolge der Durchführung einer Division mit mehreren Divisoren eine Rolle spielt - also ob beliebig Klammern gesetzt werden dürfen?
Beispiel:
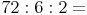
Rechengang 1: Es wird von links nach rechts gerechnet (richtiger Lösungsweg!)

Rechengang 2: Die beiden Divisoren werden vertauscht

Rechengang 3: Der Dividend und der erste Divisor werden zuerst gerechnet
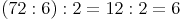
Rechengang 4: Die beiden Divisoren werden zuerst gerechnet
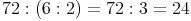
Bei den vier Rechenvarianten kommen wir nicht immer zum selben Ergebnis!
Beim Dividieren dürfen wir zwar die Reihenfolge der Divisoren vertauschen (wenn mehrere vorhanden), aber nicht beliebig Klammern setzen. Das Assoziativgesetz (= Verbindungsgesetz) gilt bei der Division also nicht!
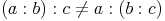
Bei einer Division dürfen nicht beliebig Klammern gesetzt werden!
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar