Herausheben gleicher Faktoren
Wir haben bereits das Distributivgesetz (= Verteilungsgesetz) hergeleitet:
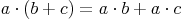
Kehren wir dieses Gesetz nun um, so können Rechnungen durch Herausheben gleicher Faktoren einfacher gemacht werden:
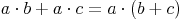
Beispiel:
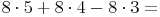
In jeder der Multiplikationen ist einer der Faktoren gleich (die Zahl 8).
Wir kehren nun das Distributivgesetz um und heben die Zahl 8 heraus:
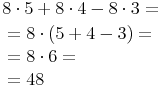
Kontrolle durch den "normalen" Rechengang:
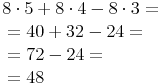
Beide Rechengänge liefern das gleiche Endergebnis, wir haben also richtig gerechnet.
Herausheben gleicher Faktoren:
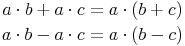
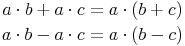
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Blonde Haare
diese seite half mir sehr weiter, um um die nötigen grundlagen zu benutzen, die ich für mein matheabitur benötige.
rechnerin
und wenn man a-a*b=x nach a auflösen will, dann geht das, indem man a heraushebt, a(1-b)=x und weiter: a=x/(1-b)