Das Distributivgesetz: Verbindung der Addition mit der Multiplikation
Beispiel:Eine Kleinschule am Land hat 4 Klassen. In jeder dieser Klassen sind jeweils 12 Burschen und 9 Mädchen.
Wie viele Schüler hat diese Schule insgesamt?
Wir schreiben uns dieses Beispiel mathematisch auf:
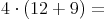
Wie berechnen zuerst die Anzahl der Schüler einer Klasse und multiplizieren diese Zahl dann mit der Anzahl der Klassen.
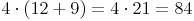
Wie berechnen zuerst die Anzahl aller Burschen und dann die Anzahl aller Mädchen und addieren die beiden Ergebnisse schlußendlich.

Beide Möglichkeiten liefern dasselbe Ergebnis: Die Schule hat insgesamt 84 Schüler.
Möglichkeit 2 wird in der Mathematik als Verteilungsgesetz (= Distributivgesetz) bezeichnet.
Distributivgesetz (Verteilungsgesetz) bei einer Summe:
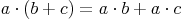
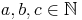
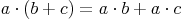
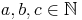
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
zeliha Cetin
super toll!