Der Nullervorteil bei der Multiplikation
Der Nullervorteil kann auch dann angewendet werden, wenn einer der mittleren Ziffern des ersten Faktors eine Null ist. Dazu vertauscht man einfach die beiden Faktoren. Dies ist ja laut dem Kommutativgesetz (Vertauschungsgesetz) bei der Multiplikation erlaubt.
Anleitung:
Schritt 1:
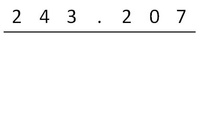
Die Multiplikation wird ganz normal aufgeschrieben.
Darunter wird ein Strich gezogen.
Schritt 2:
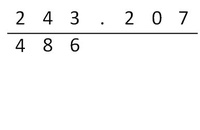
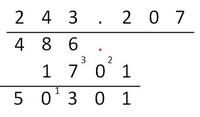
Dann wird mit dem ersten Stellenwert (bei uns mit den Hundertern) ganz normal multipliziert.
Schritt 3:
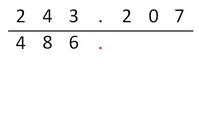
Anstatt man nun jede Ziffer des ersten Faktors mit Null multipliziert (wo ohnehin wiederum 0 herauskommt - was bei der anschließenden Addition dann nicht wichtig ist), lässt man diesen Schritt aus.
Um allerdings stellenwertrichtig zu handeln, macht man neben dem vorherigen Ergebnis einen Punkt.
Schritt 4:
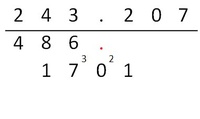
Nun wird wieder ganz normal mit der Einerziffer des zweiten Faktors multipliziert. Dazu muss natürlich wiederum nach dem Punkt um eine Stelle nach rechts gerückt werden.
Schritt 5:
Anschließend wird darunter ein Strich gezogen. Um die Multiplikation zu beenden, werden nun noch die beiden Ergebnisse addiert.
Ist einer der mittleren Ziffern des zweiten Faktors eine Null, so wird dann anstatt der Multiplikation mit Null einfach der Stellenwert um eine Stelle nach rechts verschoben (z.B. durch einen Punkt).
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Klitschko
Es war gut