Besonderheiten beim Quadratwurzelziehen I
Beispiele::
Berechnen Sie die folgenden Quadratwurzeln!
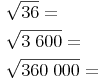
Wir lösen mit dem Taschenrechner:
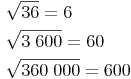
Endet ein Radikand mit zwei, vier, sechs, ... Nullen und bilden die Ziffern davor eine Zahl, deren Quadratwurzel zu einer ganzzahligen Lösung führt, so zieht man einfach die Wurzel aus der Zahl der Ziffern bis zu den Nullen und hängt dann für jeweils zwei Nullen eine Null am Endergebnis an.
z.B.: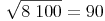
weil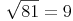 und für je 2 Nullen wird 1 Null am Ergebnis angehängt!
und für je 2 Nullen wird 1 Null am Ergebnis angehängt!
z.B.:
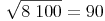
weil
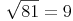 und für je 2 Nullen wird 1 Null am Ergebnis angehängt!
und für je 2 Nullen wird 1 Null am Ergebnis angehängt!
Besonderheiten beim Quadratwurzelziehen II
Beispiele::
Berechnen Sie die folgenden Quadratwurzeln!
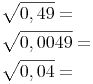
Wir lösen mit dem Taschenrechner:
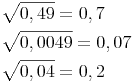
Ist der Radikand eine Dezimalzahl <1, so kann man versuchen, je 2 Nachkommastellen vom Komma aus zusammenzufassen. Aus zwei Nullen wird dabei eine Null, ebenso kann man die Wurzel aus der Zahl, die sich aus zwei Ziffern bildet, ziehen.
z.B.: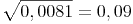
weil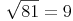 und aus 2 Nullen wird 1 Null!
und aus 2 Nullen wird 1 Null!
z.B.:
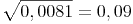
weil
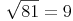 und aus 2 Nullen wird 1 Null!
und aus 2 Nullen wird 1 Null!
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar