Quadratwurzelziehen von Produkten
Hier wollen wir folgende Gesetzmäßigkeit überprüfen:
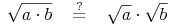
Es gilt: 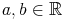
Prüfen Sie, ob das =Zeichen korrekt gesetzt wurde oder nicht!
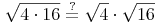
Nun berechnen wir gleichzeitig sowohl die linke als auch die rechte Seite des =Zeichens:
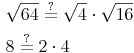
Die beiden Ergebnisse stimmen überein, daher können wir nun das ? über dem =Zeichen weglassen:

Quadratwurzelziehen von Produkten:
Multipliziert man die Quadratwurzeln zweier Zahlen, so erhält man dasselbe Ergebnis wie beim Quadratwurzelziehen des Produktes der beiden Zahlen:
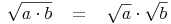
Multipliziert man die Quadratwurzeln zweier Zahlen, so erhält man dasselbe Ergebnis wie beim Quadratwurzelziehen des Produktes der beiden Zahlen:
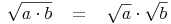
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Anica Keskic
Ich finde die Übungen sehr gut und ich finde es auch gut das es dan erklärt dasteht