Das Quadratwurzelziehen
Beispiel 1:Berechne den Flächeninhalt A eines Quadrates, dessen Seitenlänge s = 7 cm gegeben ist:
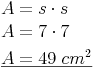
Berechne die Seitenlänge s eines Quadrates, dessen Flächeninhalt A = 81 cm² gegeben ist:
Da die Flächeninhaltsformel des Quadrates 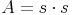 lautet, suchen wir nun also eine Seitenlänge, die mit sich selbst multipliziert 81 ergibt. Durch Probieren oder Kennen des "Kleinen 1x1" kommt man auf die richtige Lösung 9.
lautet, suchen wir nun also eine Seitenlänge, die mit sich selbst multipliziert 81 ergibt. Durch Probieren oder Kennen des "Kleinen 1x1" kommt man auf die richtige Lösung 9.
Die Seitenlänge s des Quadrates beträgt 9 cm.
Quadratwurzelziehen:Beim Quadratwurzelziehen suchen wir nun also eine positive Zahl, die mit sich selbst multipliziert die gegebene Zahl ergibt.
Für das Quadratwurzelziehen einer Zahl x schreiben wir:
![\begin{align} & \sqrt{x} \\ & \sqrt[2]{x} \\ \end{align} \begin{align} & \sqrt{x} \\ & \sqrt[2]{x} \\ \end{align}](/media/formulas/bf1cb7d1df3bf29976cec28cbe91571a.png)
Man spricht: "Wurzel aus x" oder "Quadratwurzel aus x"
Jene Zahl unter dem Wurzelzeichen wird als Radikand bezeichnet.
Weitere Beispiele:
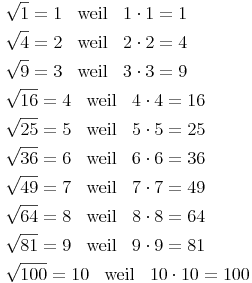
usw.
Das Quadratwurzelziehen ist die Umkehrung des Quadrierens.
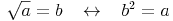
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar