Teilweises Wurzelziehen (Partielles Wurzelziehen)
Beispiel:
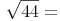
Wir zerlegen die Zahl 44 in ein Produkt, wobei ein Faktor davon eine Quadratzahl sein soll.
4 ist eine Quadratzahl, da 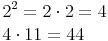
Daher gilt:
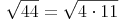
Wir wenden nun folgende Gesetzmäßigkeit an:
Quadratwurzelziehen von Produkten:
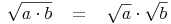
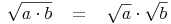
Weitere Infos: Quadratwurzel ziehen
Diese Regel übertragen wir nun auf unser Beispiel:
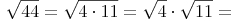
Nun können wir partiell (teilweise) Wurzelziehen:
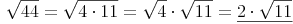
Teilweises Wurzelziehen (Partielles Wurzelziehen:
Wenn unter dem Wurzelzeichen Faktoren stehen, die Quadratzahlen sind, so kann man die Wurzel ziehen.
Wenn unter dem Wurzelzeichen Faktoren stehen, die keine Quadratzahlen sind, so bleiben sie unter dem Wurzelzeichen stehen.
z.B.: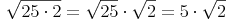
Weitere Beispiele:Wenn unter dem Wurzelzeichen Faktoren stehen, die Quadratzahlen sind, so kann man die Wurzel ziehen.
Wenn unter dem Wurzelzeichen Faktoren stehen, die keine Quadratzahlen sind, so bleiben sie unter dem Wurzelzeichen stehen.
z.B.:
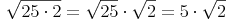
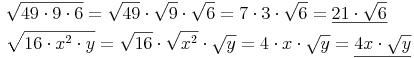
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
andrea schneider
ich würde eigentlich mehr aufgaben dazu geben
Alex
Gut erklärt. Ich hab es verstanden.
Luke
Gut erklärt! :)
Endlich hab ich's verstanden xD
Kann ich echt nur weiterempfehlen!
elli
Ahhh!!!Ok ,wenn man es verstanden hat ,dann ist es wirklich einfach!!!!
Danke :)
jo ho
gut
Jasmin
Echt super erklärung schreiben morgen Mathe und jetzt habe ich es endlich verstanden.
Groffel
Zu wenig Beispiele
Pieps
danke, habs verstanden.
Eigentlich echt voll easy ^-^
Stefan Klotz
Sehr gut erklärt!!!
Daniel
Sehr gut erklärt (Y)
Danke
Hello3
Bei solchen Zahlen wie z.B. 49 oder so versteh ich es ja auch noch aber so mit 744 oder so? Versteh ich garnicht! :(
Ndricim
das ist schon sehr verständlich jedoch in meinem Mathebuch sind viel schwierigere Aufgaben
z.B.:Wurzel von ab²c³ oder die wurzel aus 3 durch 16
Michael der Vanilla
Gut erklärt! :)
Ich habe es jetzt teilweise auch verstanden!
jake
dafür gibts dann den rechner
Nico Raith
Es hat mir echt geholfen schreibe demnächst die Mathe Abschluss prüfung und wusste nicht wie es geht macht weiter so! ;)
Niklas
Endlich verstanden
Tobias Prigge
Also meine lehrerin hat es mir 3 mal erklärt und habe es nicht verstanden aber jetzt check ich das!
Baltasar
ich habe es nd verstanden da es nd gut beschrieben wurde
Hello4
Da geb ich Hello3 auch nur recht... Mit gößeren Zahlen ist das schwieriger .-.
Josie
Hätte gerne mehr Bsp, dennoch habe ich es jetzt verstanden
Julian
Tolle erklärung aber wie wendet man sie bei zahlen wie 175 an?
Hermann
175 lässt sich unter der Wurzel zerlegen in 25 . 7
Von 25 kann man die Wurzel dann ziehen ...
Tobi
1A Erklärt
Hugo Müller
Bitte einen Rechner für Partielles Wurzelziehen einbauen! Danke