Höhensatz

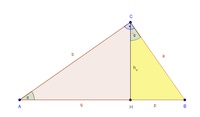
Multipliziert man die beiden Hypotenusenabschnitte, so erhält man die Höhe c hoch 2

Höhensatz

Das Dreieck BCH ist dem Dreieck ACH ähnlich, weil die beiden Winkel ( $\alpha$ ) gleich groß sind.

$\triangle{BCH} \sim \triangle{ACH}$

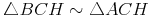
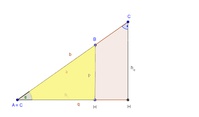
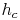Legt man nun die beiden Dreiecke so übereinander, dass die beiden Winkel $\alpha$ übereinander liegen und die Höhe h_c auf der Seite c liegt, so kann man erkennen, dass sich die beiden Dreiecke ähnlich sind und nur durch ihre Größe unterscheiden.

Bei ähnlichen Dreiecken lassen sich Verhältnisse aufstellen (Strahlensatz):

Im Dreieck ACH verhält sich die Seite q zur Höhe h im selben Winkel wie im Dreieck BCH die Höhe h zur Seite p:

q : h = h : p

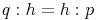
Schreiben wir dieses Verhältnis nun als Bruch an: 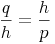$\frac{q}{h} = \frac{h}{p}$

Bringen wir die eine Höhe h auf die andere Seite: 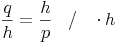$\frac{q}{h} = \frac{h}{p}\quad / \quad \cdot h$

Bringen wir nun die Seite p auf die andere Seite: 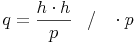$q = \frac{h \cdot h}{p}\quad / \quad \cdot p$

Schreiben wir 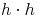$h \cdot h$ noch eleganter an: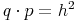 $q \cdot p = h^2$

Kathetensatz für die Kathete a:

$h^2 = p \cdot q$

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
2,2
61 Bewertungen

Kommentar #36298 von Nazao 18.02.17 20:21 Nazao: Wie kann man im höhensatz dreieck die a,b und c berechnen?