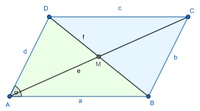
Diagonalen des Parallelogramms
Allgemeines
Unter einer Diagonale versteht man in der ebenen Geometrie die Verbindungsstrecke von nicht benachbarten Eckpunkten.
In einem Viereck lassen sich jeweils 2 gegenüberliegende Eckpunkte miteinander verbinden; somit hat jedes Viereck zwei Diagonalen - auch das Parallelogramm.
Eigenschaften
Beschriftung:
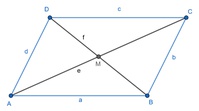
Die Diagonale vom Eckpunkt A zum Eckpunkt C wird mit e beschrifttet. Die Diagonale vom Eckpunkt B zum Eckpunkt D wird mit f beschriftet.
Länge:
Die beiden Diagonalen e und f sind unterschiedlich lang.
Schnittpunkt:
Die beiden Diagonalen schneiden einander im Schnittpunkt M, der auch das Symmetriezentrum des Parallelogramms ist.
Halbierung:
Die beiden Diagonalen halbieren einander.
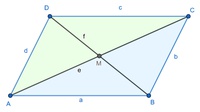
Jede Diagonale halbiert das Parallelogramm in jeweils zwei gleich große (gleichsinnig kongruente) Dreiecke.
Länge der Diagonalen (Oberstufe)
Die Längen der beiden Diagonalen lassen sich mit Hilfe des Kosinussatzes berechnen.
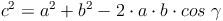
für ein Dreick mit den Seitenlängen a, b und c sowie dem von den Seiten a und b eingeschlossenen Winkel
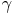 .
.
Diagonale e berechnen:
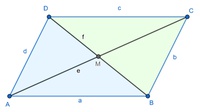
Dazu nutzen wir das Dreieck, welches die Eckpunkte A, B und C einschließt.
Die Seiten dieses Dreiecks heißen a, b und e. Der von den Seiten a und b eingeschlossene Winkel heißt Beta.
Wir wenden den Kosinussatz an: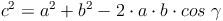
Nun ersetzen wir die Seiten und Winkel: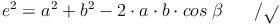
Wurzel ziehen: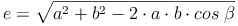
Diagonale f berechnen:
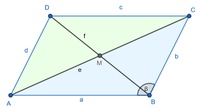
Dazu nutzen wir das Dreieck, welches die Eckpunkte A, B und D einschließt.
Die Seiten dieses Dreiecks heißen a, d=b und f. Der von den Seiten a und b eingeschlossene Winkel heißt Alpha.
Wir wenden den Kosinussatz an: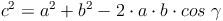
Nun ersetzen wir die Seiten und Winkel: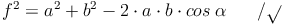
Wurzel ziehen: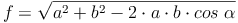
Die Diagonalen eines Parallelogramms werden mit e und f beschriftet, sind unterschiedlich lang, halbieren einander, teilen das Parallelogramm jeweils in 2 gleich große Dreiecke und schneiden einander im Symmetriepunkt M.
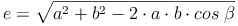
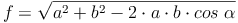
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar