Der Flächeninhalt des Parallelogramms
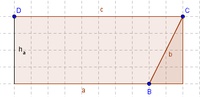
Herleitung der Flächeninhaltsformel:1) Wir konstruieren ein beliebiges Parallelogramm.
2) Nun wird die Höhe auf die Seite a so eingezeichnet, dass sie den gegenüberliegenden Eckpunkt D berührt
3) Das so entstandene Dreieck wird "abgeschnitten" und auf der anderen Seite wieder dazugegeben.
4) Ein Rechteck ist entstanden, dessen Fläche noch immer so groß ist wie jene des ursprünglichen Parallelogramms.
5) Berechnung der Fläche des Rechtecks:

Die Länge des Rechtecks entspricht der Seite c, die Breite der Höhe ha:
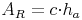
Da die Seite c genauso lang ist wie die Seite a, ergibt sich:
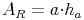
Die Fläche des Rechtecks ist genauso groß wie jene des Parallelogramms:
Flächeninhalt des Parallelogramms:
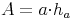
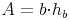
Flächeninhalt = Seite x zugehörige Höhe
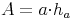
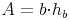
Flächeninhalt = Seite x zugehörige Höhe
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar


alexander urch
Gute Seite. Danke. Wollte noch auf einen kleinen Rechtschreibfehler aufmerksam machen: Bei der Flächenberechnung des Parallelogramms steht "dazugehöhrige Höhe". Da ist ein "h" zu viel.
lG
A. Urch
admin
Vielen Dank,
der Fehler ist bereits behoben. Solche Hinweise helfen uns enorm, Tipp- und Rechenfehler schnell aufzuspüren.
BananenDame
War mir sehr hilfreich, danke mathe-lexikon.at ;)
goldentedd
Das hat mir nur ein bisschen geholfen. Hier sind zu viele Formeln und so zeugs
Cellibelli
mir half die Seite auch supiii!!!
ich werde jetzt öfter auf www.mathe-lexikon.at gehen ;);)
Kuhmädl
mir half die seite überhaupt nicht wegen den ganzen FRomeln und so....
barby
gut
Kuhbauer
Mir half die Seite überhauptnicht zu viele Formeln :(
dernichtskönner
Schade, ;_; Mir half nicht's! :( Naja mein Name sagt alles... :(
Bonny SCHATZI
Sehr gute Seite man kann alles eingeben was man will und dann kommen schon die Antworten.
SUPI TOLLE SEITE!!!
MorgenMA-SA
ich hab morgen mathe sa und ler erst jetzt dafür hilfeeee betet das es ne 4 wird :((((( SEITE HAT MIR SEHR GEHOLFEN ;)
Viola
SEHR GUT!Mir half diese tolle seite sehr!
Anonym
Also nicht sehr hilfreich wenn ich eingebe: Umkehrformeln KreisRing und es kommt was anderes und ich finde die Seite auch nicht sehr genau würd auch den Chat nicht so groß machen kommt nicht so gut an. Meiner Meinung nach. War ein Feedback!
Dennis B.
Danke echt tolle seite habt ihr hier gemacht hilft mir sehr!! Danke!!! LG Dennis B.
Hugo
ich verstehe nicht wo hb ist. a.ha=A ist mir klar aber
b.hb=A bitte wo ist hb?