Inkreis

Wir versuchen hier anhand eines konkreten Beispiels herauszufinden, ob man einem Parallelogramm einen Inkreis zeichnen kann oder nicht.

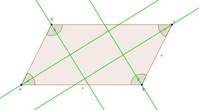
Um den Inkreis zu erhalten, müssen die Winkelsymmetralen des Parallelogramms konstruiert werden.

Die Winkelsymmetrale halbiert einen Winkel.

Konstruiert man die Winkelsymmetralen aller vier Winkel des Parallelogramms, so erkennt man, dass sich diese nicht genau in 1 Punkt schneiden.

Es gibt also keinen Punkt, dessen Normalabstand zu allen 4 Seiten gleich ist - es gibt keinen Inkreismittelpunkt.

Deshalb ist es auch nicht möglich, einen Inkreis zu konstruieren.

Ein Parallelogramm besitzt also keinen Inkreis.

Der Inkreis eines Parallelogramms:

Ein Parallelogramm besitzt keinen Inkreis.