Die Länge der Seite a einer Raute (eines Rhombus) berechnen
Die Formel zur Berechnung der Länge der Seite a in einer Raute (in einem Rhombus) lässt sich mit Hilfe des herleiten.
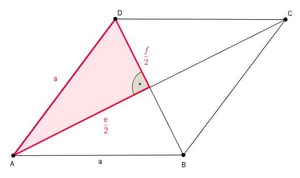
Wir konstruieren beide Diagonalen und können erkennen, dass diese die Raute in vier gleich große rechtwinklige Dreiecke teilen. Zur Herleitung der Formel konzentrieren wir uns auf eines der gleich großen Dreiecke und wenden hier den Lehrsatz des Pythagoras an.
Herleitung der Formel:
Die längste Seite zum Quadrat ist gleich der Summe der zweiten Seite zum Quadrat und der dritten Seite zum Quadrat:
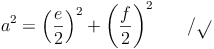
Anschließend muss noch die Wurzel gezogen werden: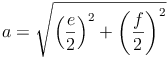
Die Länge der Seite a einer Raute (eines Rhombus) berechnen:
Die Diagonalen teilen die Raute in 4 gleich große rechtwinkelige Dreiecke, wodurch sich die Länge der Seite a mit Hilfe des Lehrsatzes des Pythagoras herleiten lässt:
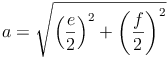
Die Diagonalen teilen die Raute in 4 gleich große rechtwinkelige Dreiecke, wodurch sich die Länge der Seite a mit Hilfe des Lehrsatzes des Pythagoras herleiten lässt:
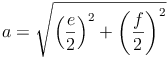
Beispiel:
geg.: Raute: e = 30 cm , f = 16 cm
ges.: a
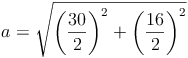

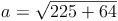
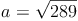
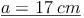
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Isabell
es hat mir geholfen