Formelsammlung Quadratische Pyramide
Eine quadratische Pyramide besteht aus einer quadratischen Grundfläche und einer Spitze. Die Eckpunkte der Grundfläche sind mit der Spitze verbunden und erzeugen dadurch 4 gleich große gleichschenklige Dreiecke.
Die Höhe steht normal auf die Grundfläche und verläuft vom Schnittpunkt der Diagonalen der Grundfläche zur Spitze der Pyramide.
Eckpunkte:
Die vier Eckpunkte der Grundfläche sind gleich weit von der Spitze entfernt:

Die vier Eckpunkte der Grundfläche sind gleich weit von der Spitze entfernt:

Kanten:
Die vier Kanten der Grundfläche sind gleich lang. Jene Kanten, die von der Grundfläche zur Spitze reichen sind ebenso gleich lang.


Die vier Kanten der Grundfläche sind gleich lang. Jene Kanten, die von der Grundfläche zur Spitze reichen sind ebenso gleich lang.


Körperhöhe:
Die Körperhöhe ist die kürzeste Verbindung vom Mittelpunkt der Grundfläche zur Spitze.
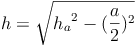
Die Körperhöhe ist die kürzeste Verbindung vom Mittelpunkt der Grundfläche zur Spitze.
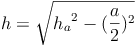
Seitenhöhe:
Die Seitenhöhe ist der kürzeste Abstand vom Mittelpunkt einer Kante der Grundfläche zur Spitze.
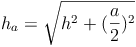
Die Seitenhöhe ist der kürzeste Abstand vom Mittelpunkt einer Kante der Grundfläche zur Spitze.
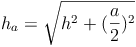
Volumen (Rauminhalt):
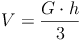
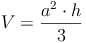
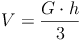
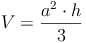
Oberfläche:
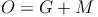
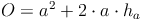 oder kürzer:
oder kürzer: 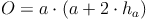
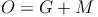
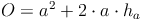 oder kürzer:
oder kürzer: 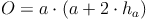
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar