Die Oberfläche der quadratischen Pyramide
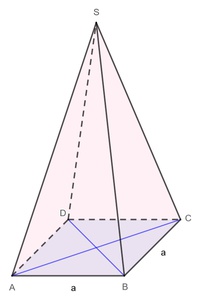
Eine quadratische Pyramide besteht aus einer quadratischen Grundfläche sowie 4 kongruente (= deckungsgleiche) gleichschenklige Dreiecke, die zusammen die Mantelfläche bilden.
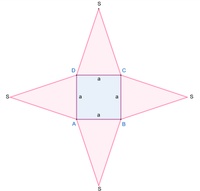
Die Oberfläche setzt sich nun aus diesen 5 Flächen (Grundfläche und Mantelfläche) zusammen:
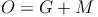
Grundfläche:
Der Name dieses geometrischen Körpers (quadratische Pyramide) bezieht sich auf die Grundfläche. Somit verrät schon der Name, dass die Grundfläche ein Quadrat ist.
Den Flächeninhalt eines Quadrates berechnet man, indem man die beiden Seitenlängen (a) miteinander multiplizierzt:
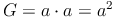
Mantelfläche:
Die Mantelfläche (kurz: Mantel) setzt sich aus den 4 Seitenflächen des Körpers zusammen. Diese 4 Seitenflächen sind gleiche (= kongruente) gleichschenklige Dreiecke.
Den Flächeninhalt eines Dreiecks berechnet man, indem man eine Seitenlänge (z.B. Kante a der Grundfläche) mit ihrer zugehörigen Höhe (Seitenhöhe ha) multipliziert und das Ergebnis durch 2 teilt. Da es sich um 4 gleiche Dreiecke handelt, muss man dies Mal 4 rechen:
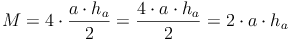
Zusammenfassung:
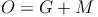

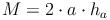
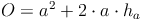
Durch Herausheben von a können wir die Formel kürzen: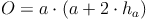
Oberfläche = Grundfläche (Quadrat) + Mantelfläche (4 kongruente gleichschenklige Dreiecke):
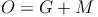
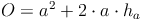 oder kürzer:
oder kürzer: 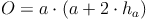
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
dc9ir
das ist die vierte webseite, in der ich volumen und oberfläche von pyramiden berechnet sehe, aber in keiner einzigen sehe ich, woher man ha (höhe des dreiecks) bekommt! natürlich ist ha² = a²/4 + h², aber ich habe sorgfältig geschaut und es nirgendwo gesehen. wird diese kenntnis denn als trivial angenommen?
(zwinker)
dc9ir