Das Netz einer quadratischen Pyramide
Faltet man eine quadratische Pyramide in der Ebene aus, so erhält man das Netz einer quadratischen Pyramide.
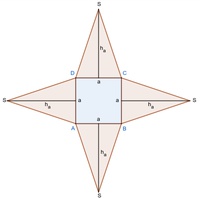
Das Netz besteht nun also aus den 5 Flächen, die die quadratische Pyramide umgeben:
Das sind die Grundfläche sowie die 4 Seitenflächen.
Die 4 Seitenflächen werden auch als Mantelflächen bezeichnet. Sie ergeben zusammden den Mantel der quadratischen Pyramide.
Bei der Grundfläche handelt es sich um ein Quadrat (daher auch die Bezeichnung "quadratische Pyramide").
Bei den 4 Seitenflächen handelt es sich um 4 kongruente (=deckungsgleiche) gleichschenklige Dreiecke.
Die 5 Seitenflächen des Netzes werden alle in wahrer Größe konstruiert. Dazu konstruiert man zuerst die Grundfläche (das Quadrat) und anschließend rundherum die 4 kongruenten gleichschenkligen Dreiecke (=Mantel).
Konstruktion:
Die Seitenlänge des Quadrates entspricht dabei der Kantenlänge der Grundfläche.
Kennt man die Seitenhöhen der Dreiecke, so kann man diese normal auf die Halbierungspunkte der Seitenkanten der Grundfläche konstruieren; kennt man die Kantenlänge eines Eckpunktes der Grundfläche zur Spitze, so kann man diese in den Zirkel nehmen, in den Eckpunkten der Grundfläche einstechen und abschlagen - so erhält man die Spitze der Dreiecke.
Die 5 Begrenzungsflächen (Quadrat und 4 kongruente gleichschenklige Dreiecke) bezeichnet man als Netz der qaudratischen Pyramide.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
amenhotep Awolaja
zeigen bitte und illustriert die quadratische netze an die kinder