Die Körperhöhe einer quadratischen Pyramide
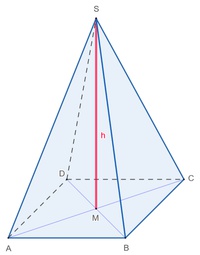
Die Körperhöhe einer quadratischen Pyramide ist der kürzeste Abstand (= Normalabstand) von der Grundfläche zur Spitze.
Jener Punkt der Grundfläche, der genau "unterhalb" der Spitze liegt und somit den kürzesten Abstand zur Spitze hat, ist der Mittelpunkt (= Schnittpunkt der Diagonalen) der quadratischen Grundfläche.
Den Mittelpunkt eines Quadrats erhält man, wenn man gegenüberliegenden Eckpunkte miteinander verbindet.
Jener Punkt, in dem sich die beiden Diagonalen des Quadrats schneiden, ist der Fußpunkt der Körperhöhe unserer quadratischen Pyramide.
Verbindet man nun diesen Fußpukt (Mittelpunkt der Grundfläche) mit der Spitze, so erhält man die Körperhöhe.
Die Körperhöhe berechnen
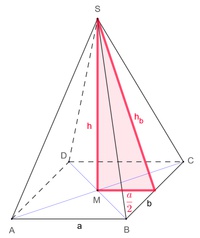
Die Körperhöhe h einer quadratischen Pyramide lässt sich mit Hilfe des "Lehrsatzes des Pythagoras" berechnen. Dazu behelfen wir uns eines rechtwinkeligen Hilfsdreiecks, welches den Mittelpunkt M der Grundfläche mit der Spitze S und dem Halbierungspunkt der Seite a verbindet.
Die Seitenlängen dieses Dreiecks sind die Körperhöhe, die Höhe des Dreiecks der Seitenfläche auf die Seite a und die Hälfte der Kante a.
Die Summe der Flächeninhalte der Kathetenquadrate ist gleich dem Flächeninhalt des Hypotenusenquadrates.
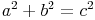
Um diesen Lehrsatz auf unser Hilfsdreieck zu übertragen, heißen die beiden Katheten in unserem Dreieck  und
und 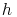 , die Hypotenuse heißt
, die Hypotenuse heißt 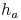 .
.
Daraus ergibt sich: 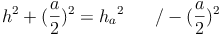
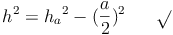
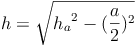
Die Körperhöhe einer quadratischen Pyramide ist der kürzeste Abstand (= Normalabstand) von der Grundfläche zur Spitze.
Sie verbindet somit den Mittelpunkt der Grundfläche mit der Spitze.
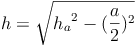
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar