Multiplizieren mit einer Zahl, die beliebig viele Nullen am Ende hat
Beispiele:Wir multiplizieren folgende Beispiele zuerst mit dem Taschenrechner, um durch die Ergebnisse dann eine allgemeine Rechenregel herzuleiten:
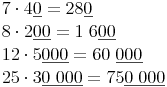
...
Wir können erkennen, dass das Ergebnis am Ende mindestens genau so viele Nullen hat wie der zweite Faktor.
Eigentlich wurde der erste Faktor mit dem 2. Faktor multipliziert, es wurden nur vorläufig die letzten Nullen des 2. Faktors weggelassen, die nach der Multiplikation wieder angehängt wurden.
Multiplikation mit einer Zahl, die beliebig viele Nullen am Ende hat:
Man multipliziert den ersten Faktor mit dem 2. Faktor, lässt von diesem allerdings die Nullen am Ende weg.
Nach der Multiplikation hängt man die Anzahl der Nullen die man weggelassen hat am Ergebnis an.
Beispiel:
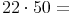
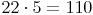
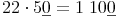
Man multipliziert den ersten Faktor mit dem 2. Faktor, lässt von diesem allerdings die Nullen am Ende weg.
Nach der Multiplikation hängt man die Anzahl der Nullen die man weggelassen hat am Ergebnis an.
Beispiel:
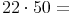
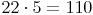
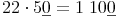
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar