Kubieren
Multipliziert man eine Zahl (eine Variable) zwei Mal mit sich selbst, so spricht man vom kubieren.
Hierbei handelt es sich um einen Spezialfall des Potenzierens , nämlich mit dem Exponenten 3!
Beispiel:
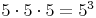
Aussprache:
Geasprochen wird: "5 hoch 3" oder "5 Kubik"
(Das Wort "kubieren" kommt daher, da das Volumen eines Würfels (lat. "cubus") durch das Multiplizieren der gleich langen Seiten a, b und h berechnet wird: 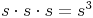 )
)
Weitere Beispiele:
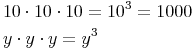
Kubieren von natürlichen Zahlen:
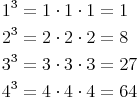
usw.
Kubieren von negativen Zahlen:
Kubiert man negative ganze Zahlen, so ist das Ergebnis immer negativ, da die Multiplikation einer negativen Zahl mit einer weiteren negativen Zahl zwar eine positvie Zahl ergibt, eine weitere Multiplikation mit einer negativen Zahl aber wiederum zu einer negativen Zahl führt:
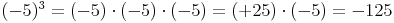
Tastatur:
Auf einer deutschen PC-Tastatur findet man das ³-Zeichen als Unterbelegung der Taste "3". Drückt man also die Taste "Alt Gr" und die Taste "3" gleichzeitig, so schreibt man die Hochzahl 3.
Unter dem Kubieren versteht man eine Multiplikation einer Zahl (einer Variablen) 2 Mal mit sich selbst. Die Hochzahl (der Exponent) beträgt also 3.
z.B.:
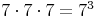
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar