Kubieren von negativen Zahlen
Beispiel:

Kubieren bedeutet, die Zahl 2 Mal mit sich selbst zu multiplizieren:

Multiplizieren von zwei negativen ganzen Zahlen:
Multipliziert man zwei negative ganze Zahlen miteinander, so ist das Ergebnis positiv.
Multipliziert man zwei negative ganze Zahlen miteinander, so ist das Ergebnis positiv.
Weitere Infos: Multiplizieren von zwei negativen ganzen Zahlen
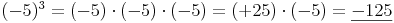
Kubieren von negativen Zahlen:
Kubiert man eine negative ganze Zahl, so ist das Ergebnis immer negativ.
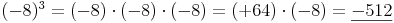
Beispiele:Kubiert man eine negative ganze Zahl, so ist das Ergebnis immer negativ.
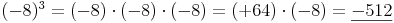

- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar