Umkehraufgaben zur Oberflächenberechnung: Berechnung der Breite
Beispiel:
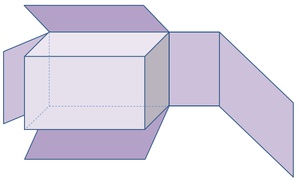
Ein Quader hat eine Oberfläche von 158cm².
Die Länge des Quaders beträgt 5cm, die Höhe beträgt 8cm.
Berechnen Sie die Breite b des Quaders!
Möglichkeit 1: In die Formel einsetzen:
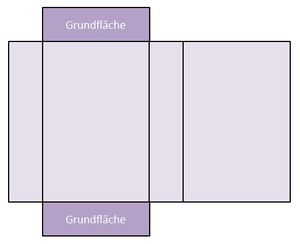
Aus dem vorherigen Kapitel wissen wir bereits, dass die Oberfläche eines Würfels die Summe aller sechs Flächen (= Quadraten) ist:
Oberfläche des Quaders:
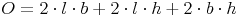
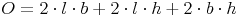
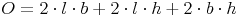
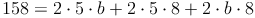
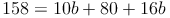
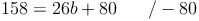
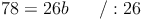

Antwort: Die Breite b des Quaders beträgt 3 cm.
Möglichkeit 2: Formel umformen:
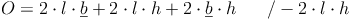
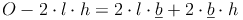
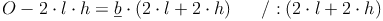
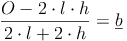
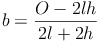
Beispiel: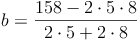
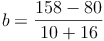
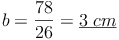
Probe: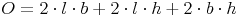
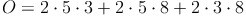
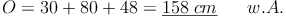
Berechnung der Breite eines Quaders, wenn die Oberfläche, die Länge und die Höhe bekannt sind:
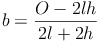
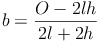
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar