Primfaktorzerlegung von natürlichen (zusammengesetzten) Zahlen
Die beste Übersicht bei der Zerlegung einer zusammengesetzten Zahl in ihre Primfaktoren erhält man beim Untereinanderschreiben. Dieses Verfahren wird Ihnen im folgenden beschrieben. Es gibt natürlich auch noch andere Schreibweisen.
Schritt 1:
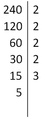
Die zusammengesetzte Zahl wird aufgeschrieben, rechts daneben eine senkrechte Linie gezogen.
Schritt 2:
Wir versuchen mit der kleinstmöglichen Primzahl zu beginnen, meistens mit 2.
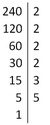
240 lässt sich durch 2 ohne Rest teilen, also schreiben wir die erste Primzahl (2) rechts neben dem senkrechten Strich an, das Ergebnis (also 120) unter 240.
Schritt 3:
120 lässt sich durch 2 ohne Rest teilen, also schreiben wir die Primzahl 2 rechts neben dem senkrechten Strich an, das Ergebnis (also 60) unter 120.
Schritt 4:
60 lässt sich durch 2 ohne Rest teilen, also schreiben wir die Primzahl 2 rechts neben dem senkrechten Strich an, das Ergebnis (also 30) unter 60.
Schritt 5:
30 lässt sich durch 2 ohne Rest teilen, also schreiben wir die Primzahl 2 rechts neben dem senkrechten Strich an, das Ergebnis (also 15) unter 30.
Schritt 6:
15 lässt sich nicht durch 2, aber durch 3 ohne Rest teilen, also schreiben wir die Primzahl 3 rechts neben dem senkrechten Strich an, das Ergebnis (also 5) unter 15.
Schritt 7:
5 lässt sich nicht durch 3, aber durch 5 ohne Rest teilen, also schreiben wir die Primzahl 5 rechts neben dem senkrechten Strich an, das Ergebnis (also 1) unter 5.
Schritt 8:
Ergebnis: 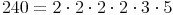
Jede natürliche Zahl, die selbst keine Primzahl ist, lässt sich eindeutig in ein Produkt von Primzahlen zerlegen.
(Eindeutig bis auf die Reihenfolge!)
z.B.:
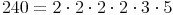
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar




M&M
Hallo! Würde das Ergebnis bei der Primfaktorzerlegung von 2049 = 3 mal 683 stimmen?
Ecaterina
Es hat mir sehr weiter geholfen den ich bin in Mexoko und dort muss man im Untericht alles alleine machen
3hardy
Widerspricht die 1 nicht dieser Regel, da sie ja keine Primzahl ist?
Daniel
@M&M ja denn:
die wurzel aus 683 ist 26,134 und bis 23 lässt sich die 683 durch keine prim ohne rest teilen.
McFlurry
Es war einfach nur falsch!!!!