Sieb des Eratosthenes
Bis heute gibt es noch keine Formel zur Ermittlung der Primzahlen. Noch niemand hat eine Regelmäßigkeit in ihrem Auftreten gefunden, deshalb muss man sich andere Hilfsmittel zur Ermittlung der Primzahlen zu Hilfe nehmen.
Eines davon ist das sogenannte Sieb des Eratosthenes, benannt nach dem griechischen Mathematiker Eratosthenes von Kyrene (276 - 194 v. Chr.)
Anleitung:
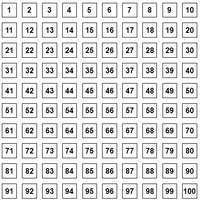
Man schreibt die Zahlen bis z.B. 100 auf (am übersichtlichsten in Reihen zu je 10 Zahlen). Dann "sieben" wir alle Zahlen aus, die durch eine andere Zahl als 1 oder sich selbst teilbar sind. Jene Zahlen, die übrig bleiben, sind schließlich die Primzahlen.
Schritt 1:
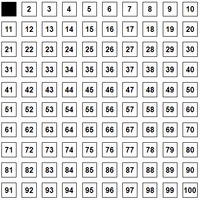
Die Zahl 1 kann gestrichen werden, da sie keine Primzahl ist.
Schritt 2:
Die Zahl 2 wird angemalt, da es sich bei ihr um eine Primzahl handelt.
Alle Vielfachen von 2 sind durch 2 teilbar, sind also keine Primzahlen. Deshalb können wir diese Zahlen durchstreichen (4, 6, 8, 10, ...)
Schritt 3:
Die Zahl 3 wird angemalt, da es sich bei ihr um eine Primzahl handelt.
Alle Vielfachen von 3 sind durch 3 teilbar, sind also keine Primzahlen. Deshalb können wir diese Zahlen durchstreichen (6, 9, 12, ...)
Schritt 4:
Die Zahl 4 ist bereits gestrichen, kann also übersprungen werden.
Die Zahl 5 wird angemalt, da es sich bei ihr um eine Primzahl handelt.
Alle Vielfachen von 5 sind durch 5 teilbar, sind also keine Primzahlen. Deshalb können wir diese Zahlen durchstreichen (10, 15, 20, ...)
Schritt 5:
Die Zahl 6 ist bereits gestrichen, kann also übersprungen werden.
Die Zahl 7 wird angemalt, da es sich bei ihr um eine Primzahl handelt.
Alle Vielfachen von 7 sind durch 7 teilbar, sind also keine Primzahlen. Deshalb können wir diese Zahlen durchstreichen (14, 21, 28, ...)
Schritt 6:
Die restlichen verbleibenden Zahlen können angemalt werden, es handelt sich dabei um die Primzahlen.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar





Ronald Hofmann
Hallo,
dieses Verfahren ist ganz nett, wenn es um nur wenige Zahlen geht wie in diesem Beispiel. Kompliziert wird es bei vielen Zahlen. Z.B. alle Primzahlen bis 150.000.000. Muss ich mir dann erst ein Array mit allen Zahlen erstellen und dann nach der beschriebenen Methode aussieben? Das dauert lange. Allein das Füllen des Arrays schon. Oder gibt es da eine andere Methode?
Grüsse, Ronald Hofmann
---
Max Weber
Hallo,
neben dem Sieb des Eratosthenes gibt es noch eine optimiertere Version davon: das Sieb von Atkin, das mit dem 60er Rest der Zahlen arbeitet und damit einige Vorarbeit leistet. Dieses Verfahren sollte schneller gehen.
Grüße, Max Weber
Catrina
Bei diesem Beispiel reicht es, wenn man es bis 7 prüft. Nimmt man Zahlen bis 200, was per Hand noch geht, reicht das aber nicht. Allgemeiner formuliert: Zahlen möglichst im Quadrat anordnen (beim Rechteck sollte die waagerechte länger sein, unvollständige Reihen sind ok, zählen aber als Reihe) und dann die Vielfachen der obersten Reihe streichen.
Sarina
Hallo!Das Sieb des Eratosthenes ist wirklich sehr praktisch.Ich habe da nur noch eine Frage:wieso heißt es eigentlich "Sieb"?
Erich Hnilica, BEd
Liebe Sarina!
Diese Methode wurde nach dem griechischen Mathematiker Eratosthenes von Kyrene benannt.
Sieb deshalb, weil wie mit einem Sieb die Zahlen ausgesiebt werden, bis nur noch die Primzahlen übrig bleiben.
Lg
Admin
Amelie
Ich finde es gut
goran
gibt es sowas ine einer schnellen programmiersprache auch als lauffähiges tool?