Parallelogramm: Seite a berechnen

Anleitung, wie Sie die Länge der Seite a eines Parallelogramms berechnen können, wenn der Umfang und die Seite b gegeben sind.

Die Seite a eines Parallelogramms berechnen, wenn der Umfang und die Seite b gegeben sind

Beispiel:
Von einem Parallelogramm kennt man die Länge der Seite b = 8 cm und den Umfang u = 28 cm. Berechnen Sie die Länge der Seite a!

Herleitung der Formel:
Aus dem vorherigen Kapitel wissen wir bereits, dass der Umfang eines Parallelogramms die Summe der vier Seiten ist. Da in einem Parallelogramm die gegenüberliegenden Seiten jeweils gleich lang sind, gilt:

Umfang des Parallelogramms:

u = 2 \cdot a + 2 \cdot b

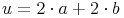
Nachdem wir den Umfang und die Seite b des Parallelogramms kennen, die Seite a allerdings nicht, formen wir unsere Formel so lange um, bis die Seite a allein auf einer Seite steht: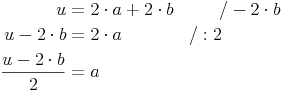

\begin{align}u & = 2 \cdot a + 2 \cdot b && \qquad / - 2 \cdot b \\ u - 2 \cdot b & = 2 \cdot a && \qqad / : 2 \\ \frac{u - 2 \cdot b}{2} & = a \end{align}

Beispiel (Forts.):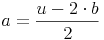

a = \frac{u - 2 \cdot b}{2}

a = \frac{28 - 2 \cdot 8}{2}

a = \frac{28 - 16}{2}

a = \frac{12}{2}

\underline{a = 6\ cm}

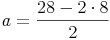
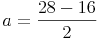
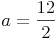
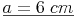
Probe: Wir setzen das Ergebnis in die Umfangsformel ein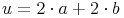

u = 2 \cdot a + 2 \cdot b

u = 2 \cdot 6 + 2 \cdot 8

u = 12 + 16

\underline{u = 28\ cm} \qquad w.A.

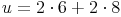
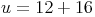
Antwort:

Die Seite a des Parallelogramms ist 6 cm lang.

Berechnung der Seite a eines Parallelogramms, wenn der Umfang und die Seite b gegeben sind:

a = \frac{u - 2 \cdot b}{2}

Kommentar verfassen