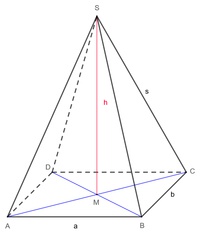
Die Kanten der rechteckigen Pyramide
In den Kanten treffen jeweils 2 Seitenflächen der rechteckigen Pyramide aufeinander.
Eine Kante verbindet 2 Eckpunkte miteinander.
Die Beschriftung der Kanten erfolgt mit für Strecken üblichen Kleinbuchstaben. Üblicherweise werden die ersten Buchstaben des Alphabets (a, b, ...) zur Beschriftung der Grundfläche verwendet. Da die Grundfläche rechteckig ist, sind die gegenüberliegenden Seiten dieser Fläche gleich lang und können somit gleich beschriftet werden: a, b, c=a, d=b
Jene Kanten, die die Eckpunkte der Grundfläche mit der Spitze verbinden, sind gleich lang und werden mit s beschriftet.
Eine rechteckige Pyramide hat insgesamt 8 Kanten, die allerdings nicht alle gleich lang sind.
Von den 4 Kanten der Grundfläche sind die jeweils gegenüberliegenden Kanten gleich lang.
Ausnahmen:
Handelt es sich bei der Grundfläche um ein besonderes Rechteck, nämlich ein Quadrat, so sind alle 4 Kanten der Grundfläche gleich lang.
Man spricht dann von einer quadratischen Pyramide, der wir ein eigenes Kapitel widmen.
Jene 4 Kanten, die die Eckpunkte der Grundfläche mit der Spitze verbinden, sind gleich lang. Daher werden diese Kanten mit demselben Keinbuchstaben (s) beschriftet. Es gilt:
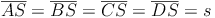
Eine rechteckige Pyramide hat insgesamt 8 Kanten.
Gegenüberliegende Kanten der Grundfläche sind gleich lang. Jene Kanten, die von der Grundfläche zur Spitze reichen sind ebenso gleich lang.

- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar