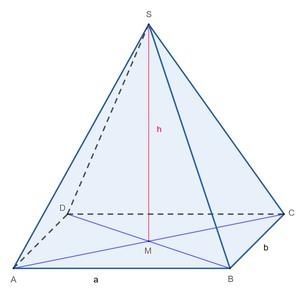
Das Volumen (der Rauminhalt) der rechteckigen Pyramide
Unter dem Volumen (oder auch Rauminhalt) eines Körpers versteht man den räumlichen Inhalt dieses Körpers.
Umgangssprachlich würde man sagen: all jenes, das in diese Pyramide hineinpasst (Flüssigkeit, ...)
Das Volumen wird mit V abgekürzt und entspricht in der ebenen Geometrie dem Flächeninhalt.
Herleitung der Formel:
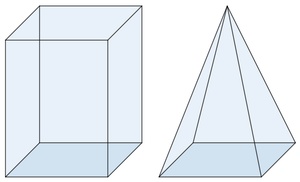
Wir gehen von einen Quader und einer Pyramide aus, die dieselbe Grundfläche (=Rechteck) und dieselbe Höhe besitzen.
Aus dem Kapitel Volumen des Quaders kennen wir bereits die Formel zur Berechnung des Volumens eines Quaders:
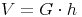
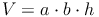
Volumen = Grundfläche (Rechteck) mal Höhe
Umschüttversuch:
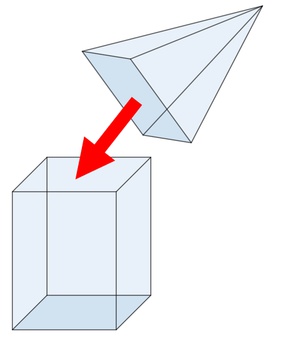
Wir füllen nun die Pyramide mit Flüssigkeit und schütten diese in den Quader mit gleicher Grundfläche und gleicher Höhe.
Diesen Vorgang kann man genau 3 Mal machen bis der Quader ganz voll ist.
Das Volumen des Quaders ist daher 3 Mal so groß wie das Volumen der Pyramide.
Oder anders ausgedrückt:
Das Volumen der Pyramide ist ein Drittel des Volumens des Quaders.
Somit müssen wir nur die Volumsformel des Quaders durch 3 dividieren, um die Volumsformel der Pyramide zu erhalten:
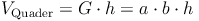
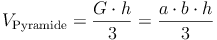
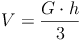
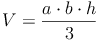
Volumen = (Grundfläche mal Höhe) : 3
Beispiel:
geg.: rechteckige Pyramide: a = 7 cm , b = 6 cm, h = 10 cm
ges.: V
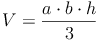
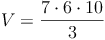
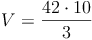
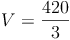
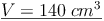
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar