Die Seitenhöhe einer rechteckigen Pyramide
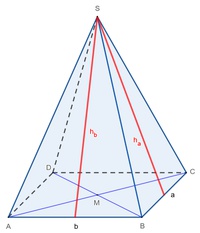
Die Seitenhöhe einer rechteckigen Pyramide ist der kürzeste Abstand (= Normalabstand) vom Mittelpunkt einer Kante der Grundfläche zur Spitze.
Somit teilt die Seitenhöhe eine Seitenfläche in zwei gleich große (= kongruente) rechtwinkelige Dreiecke.
Nachdem je zwei gegenüberliegende Seitenflächen einer rechteckigen Pyramide gleich groß sind und somit auch je zwei Kanten der Grundfläche (a und b) gleich lang sind, gibt es zwei unterschiedlich lange Seitenhöhen (h_a, h_b).
Die Seitenhöhe auf die Kante b berechnen
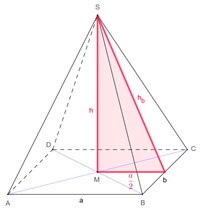
Die Seitenhöhe h_b einer rechteckigen Pyramide lässt sich mit Hilfe des "Lehrsatzes des Pythagoras" berechnen. Dazu behelfen wir uns eines rechtwinkeligen Hilfsdreiecks, welches den Mittelpunkt M der Grundfläche mit der Spitze S und dem Halbierungspunkt der Seite b verbindet.
Die Seitenlängen dieses Dreiecks sind die Körperhöhe (h), die Höhe des Dreiecks der Seitenfläche auf die Seite b (h_b) und die Hälfte der Kante a (a/2).
Um diesen Lehrsatz auf unser Hilfsdreieck zu übertragen, heißen die beiden Katheten in unserem Dreieck  und
und 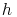 , die Hypotenuse heißt
, die Hypotenuse heißt 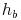 .
.
Daraus ergibt sich: 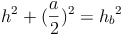
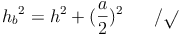
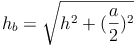
Die Summe der Flächeninhalte der Kathetenquadrate ist gleich dem Flächeninhalt des Hypotenusenquadrates.
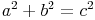
Die Seitenhöhe auf die Kante a berechnen
Genauso lsst sich natürlich die Formel zur Berechnung der Seitenhöhe auf die Kante a herleiten.
Um diesen Lehrsatz auf unser Hilfsdreieck zu übertragen, heißen die beiden Katheten in unserem Dreieck  und
und 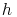 , die Hypotenuse heißt
, die Hypotenuse heißt 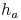 .
.
Daraus ergibt sich: 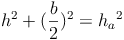
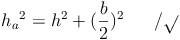
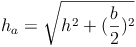
Die Seitenhöhe einer rechteckigen Pyramide ist der kürzeste Abstand (= Normalabstand) vom Mittelpunkt einer Kante der Grundfläche zur Spitze.
Eine rechteckige Pyramide hat zwei unterschiedlich lange Seitenhöhen.
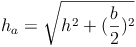
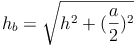
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar