Teilbarkeit durch 7
Für die Teilbarkeit durch 7 gibt es mehrere unterschiedliche Teilbarkeitsregeln.
Wir zeigen Ihnen auf dieser Seite eine der aus unserer Sicht einfachereren Teilbarkeitsregeln durch 7.
Beispiel:
Prüfen Sie, ob die Zahl 17059 durch 7 teilbar ist oder nicht.
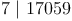 oder
oder 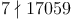 ?
?
Schritt 1:
Wir teilen die Zahl in zwei Teile: ihre letzte Ziffer b und den Rest a: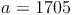 und
und 
Schritt 2:
Wir subtrahieren nun zwei Mal die letzte Ziffer b vom Rest a: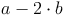
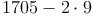
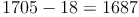
Schritt 3:
Wir wiederholen diesen Vorgang so oft, bis wir auf eine (möglichst kleine) Zahl kommen, bei der wir im Kopf einfach feststellen können, ob sie durch 7 teilbar ist oder nicht.
Ausgangszahl aus Schritt 2: 1687 und
und 
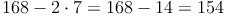
Schritt 4:
Ausgangszahl aus Schritt 4: 154 und
und 

Schritt 5:
7 ist durch 7 teilbar! Somit ist auch die Zahl 17059 durch 7 teilbar.
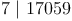
Eine Zahl ist durch 7 teilbar, wenn auch jene Zahl durch 7 teilbar ist, die entsteht, wenn man das Doppelte der letzten Ziffer von der restlichen Zahl subtrahiert.
(Tipp: So lange wiederholen, bis eine möglichst kleine Zahl entsteht!)
z.B. 315 ist durch 7 teilbar, weil:
a = 31 und b = 5
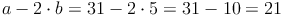
21 ist durch 7 teilbar, daher ist auch die Zahl 315 durch 7 teilbar!
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Paul
Wie teilt man durch 7,
wenn
die letzte Ziffer eine 0 ist??????
F. Roggmann
Es geht viel einfacher und schneller vor allem.
46126650212524
46 126650212524
-
42 000000000000 -> definitiv durch 7 teilbar, kann also weg in den Müll.
was bleibt?
4 126650212524
41 26650212524
(41)Die ersten beiden Zahlen wieder zusammenziehen. Wie oft passt die 7 hier rein? Richtig 5 x (35)Rest? 6
-
35 00000000000
6 26650212524
62 6650212524
-
56 0000000000
6 6650212524
66 650212524
(66)
-
3 650212524
36 50212524
(36) 5x passt sie rein Rest 1
1 50212524
15 0212524
(15) 2x Rest 1
1 0212524
10 212524
(10) 1x Rest 3
3 212524
32 12524
(32) 4x Rest 4
4 12524
41 2524
(41) 5x Rest 6
6 2524
62 524
(62) 8x Rest 6
6 524
65 24
65:7=9 Rest 2
2 24
22 4
22:7=3 Rest 1 Die eins wieder nach vorne...
14 -> geht durch 7 also! oops ^^ fertig.
46126650212524 ist durch 7 teilbar Punkt fertig aus.
Auf diese Weise könnt ihr in Sekunden/Minuten die teilbarkeit einer Zahl beliebiger Größe durch 7 testen.
Vorteil der methode gegenüber obigem: wir schmeißen größere Stückchen weg und kommen daher schneller an´s Ziel.
Sicher gibt´s die Methode schon irgendwo, hab sie mir auch gerade nur ausgedacht als ich das umständliche Gekrakel da oben sah mit dem man sicher jeden Schüler zur Weißglut quälen kann.
Ich habe fertig.
Johannes
Die Regel zur Teibarkeit durch 7 ist mathematisch ganz nett. In der Praxis macht es wenig Sinn sie anzuwenden, da es genauso schnell geht, die Zahl gleich durch 7 zu teilen und dabei festzustellen ob ein Rest bleibt.
Frank
Für mich sind alle Teilbarkeitsregeln durch 7 Quatsch. Eine ganz gewöhnliche schriftl. Division durch 7 ist der kürzeste und schnellste Weg. Jede Regel ist hier eine Verlängerung des Weges und damit sinnlos.
Eric Wutzke
Die Methode von F. Roggmann ist sehr interessant. Man vollführt also eine komplette schriftliche Division durch 7 ohne sich das Ergebnis aufzuschreiben ;-)
Albania
Kann man trm nicht kapieren also ich checke es immer noch nichtt
C. Schuhmacher
Man nimmt immer zwei Ziffern modulo 7 und multipliziert das Modulo-Ergebnis mit 2. Das Ergebnis wird zu den nächsten zwei Ziffern addiert usw. Ist das Ergebnis 0 ist die Zahl durch 7 teilbar. Bei Zahlen mit ungerader Ziffernanzahl wird mit nur der ersten Ziffer begonnen.
Also: 46126650212524
Erste Ziffern = 46 => 4 (Rest zur nächsten 7er Zahl) x 2 = 8
Die nächsten Ziffern sind 12. 12 plus 8 ist 20. 20 modulo 7 ist 6 mal 2 ist 12.
66+12 => 1 50+2 => 3 21+6 => 6 25+12 => 2 24+4 => 0 fertig.
Hannah
Man kann auch immer die letzten 3 Ziffern von den vorderen Ziffern abziehen, da ist man bei größeren Zahlen schneller ;)
Bsp.: 6044211341
6044211-341 = 6043870
6043-870 = 5173
5-173 = -168
jetzt könnte man noch weiter den Trick von oben anwenden, also 16 - 2*8 = 0
oder man rechnet hier schnell durch 7:
168:7 = 24
-> 6044211341 ist durch 7 teilbar.
aber ja, es stimmt schon, dass diese Tricks nicht wirklich schneller sind, als die Zahl einfach per schriftlicher Division durch 7 zu rechnen
Georg Kwossek
Hannahs Beispiel ist besser, als sie selber denkt. Ihre Rechnung zeigt nämlich nicht nur, dass 6044211341 durch 7 teilbar ist, sondern auch dass diese Zahl durch 11 und 13 nicht teilbar ist.
Dazu muss man wissen, was man tut, wenn man die von Hannah beschriebene Rechnung durchführt. Man subtrahiert hier immer ein Vielfaches des Produkts von 7, 11 und 13. 7 x 11 x13 ergibt 1001.
Nehmen wir als Beispiel die Zahl 17.108. Ziehen wir die letzten drei Zahlen ab, ergibt das -91. Das Vorzeichen ist egal, ich komme auch auf die 91, wenn ich die ersten beiden Zahlen von den letzten drei abziehe. An dieser zweiten Rechnung lässt sich allerdings klarer darstellen, dass ich die Subtraktion 17.108 - 17.017 durchgeführt habe. 17.017 ist 7 x 11 x13 x 17, also ein Vielfaches von 7 x 11 x13.
Hannas Trick beinhaltet also auch eine Probe für die Teilbarkeit einer Zahl durch 11 und 13.
Dave
Die Teilbarkeitsregel scheint erst ab einer bestimmten Größe anwendbar zu sein..bei 105 z. B. funktioniert sie noch nicht! 10-2x5= 10-10= =0
Thorsten
Es scheint eine neue Regel zu geben, die kürzlich von Chika Ofilih entdeckt wurde: eine Zahl ist durch 7 teilbar, wenn man ihre letzte Stelle mit 5 multipliziert und das Ergebnis zur restlichen Zahl (alle Stellen außer der letzten) addiert. Probieren wir's gleich mal aus mit dem Beispiel von Hannah, 6044211341.
604421134 + 5 * 1
= 604421139
60442113 + 5 * 9
= 60442158
6044215 + 5 * 8
= 6044255
604425 + 5 * 5
= 604450
60445 + 5 * 0
= 60445
6044 + 5 * 5
= 6069
606 + 9 * 5
= 651
65 + 5 * 1
= 70
Ergebnis: ja.
Sind natürlich immer noch recht viele Schritte, aber die Addition leichter als die Subtraktion.
Edith Spocinska
Wenn Sie prüfen möchten, ob eine Zahl durch 7 teilbar ist, können Sie auf eine Teilbarkeitsregel zurückgreifen, bei der Sie ein einfaches Verfahren durchführen. 1. Dazu müssen Sie die erste Ziffer der Zahl mal 3 rechnen und anschließend die nächste Ziffer addieren. 2. Diese Summe müssen Sie erneut mit 3 multiplizieren und mit der folgenden Ziffer addieren. 3. Dies müssen Sie so lange durchführen, bis Sie die letzte Ziffer addiert haben
Marc
Sieht so aus als ist jeder Test komplizierter als die Berechnung selber und fordert auch so viele Handlungen wie es Ziffern im Zahl gibt.
Philip
@Dave: 10-10=0 und 0 kann man durch 7 teilen. Also kann man auch 105 durch 7 teilen.
Karl die Maschine
Kluge Leute die hier unterwegs sind. Ich find Hannahs Lösung immer noch am schönsten, auch wenn der Taschenrechner viel schneller ist...
Julischki
Die Teilbarkeitsregel stimmt doch gar nicht. 49:7 --> 49 - 18 = 31 --> 31 ist nicht durch 7 teilbar, 49 aber sehr wohl.
Erich Hnilica, BEd
Liebe/r Julischki!
Du musst das Doppelte der letzten Ziffer (2 mal 9 = 18) von der restlichen Zahl (4) abziehen: 4 - 18 = -14 --> ist durch 7 teilbar, somit ist auch 49 durch 7 teilbar!