Parallelogramm - Konstruktion
geg.: Parallelogramm:
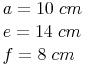
ges.: Konstruktion
Zeichnen Sie zuerst eine Skizze des Parallelogramms und beschriften Sie dieses vollständig (Seiten, Eckpunkte, Winkel).
Die gegebenen Bestimmungsstücke werden nun färbig markiert, um nachher die Konstruktion einfacher durchführen zu können.
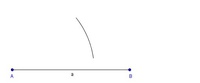
Beginnen Sie mit der Konstruktion der Seite a = 10cm, welche die Eckpunkte A und B miteinander verbindet.
Beschriften Sie die gezeichnete Seite und die beiden Eckpunkte.
Aus der Skizze kann man erkennen, dass wir den 1. Teil der Konstruktion über das Hilfsdreieck ABM machen müssen (M = Mittelpunkt).
Da in einem Parallelogramm der Mittelpunkt sowohl die Diagonale e als auch die Diagonale f genau in der Mitte teilt, ergeben sich folgende Längen: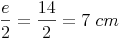
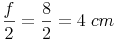
Aus der Skizze kann man erkennen, dass die Diagonale e vom Eckpunkt A ausgeht.
Konstruktion des Hilfsdreiecks:
Nehmen Sie die Länge der halben Diagonale e (7 cm) in den Zirkel, stechen Sie im Eckpunkt A ein und ziehen Sie einen beliebig langen Kreisbogen mit dem Radius r = 7 cm.
Aus der Skizze kann man erkennen, dass die Diagonale f vom Eckpunkt B ausgeht.
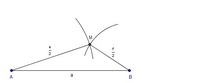
Nehmen Sie deshalb die Länge der halben Diagonale f (4 cm) in den Zirkel, stechen Sie im Eckpunkt B ein und ziehen Sie einen beliebig langen Kreisbogen mit dem Radius r = 4 cm.
Der Schnittpunkt der beiden Kreisbögen ergibt laut Skizze den Mittelpunkt M.
Verbinden Sie diesen mit den beiden anderen Eckpunkten, um das Hilfsdreieck (die erste Hälfte des Parallelogramms) fertigzustellen.
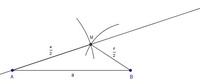
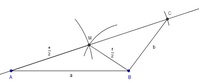
Um den 2. Teil des Parallelogramms zu bekommen, verlängern Sie die halbe Diagonale e nach oben.
Nachdem der Mittelpunkt die Diagonale e in 2 gleich lange Teile teilt, liegen die Eckpunkte A und C gleich weit von M entfernt.
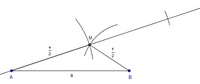
Stechen Sie mit dem Zirkel in den Mittelpunkt M ein, spannen Sie ihn bis zum Eckpunkt A und schlagen Sie diese Länge auf der Verlängerung der halben Diagonale e ab.
Verbinden Sie nun den entstandenen Eckpunkt C mit dem Eckpunkt B, Sie erhalten somit die Seite b.
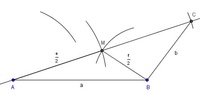
Es ist nun ein neues (größeres) Hilfsdreieck ABC entstanden, welches nur noch gespiegelt gehört, um das Parallelogramm fertig zu zeichnen.
Da die Seite d genauso lang ist wie die Seite b, nehmen Sie die Länge der Seite b in den Zirkel. Da die Seite d vom Eckpunkt A ausgeht, stechen Sie im Eckpunkt A ein und ziehen Sie einen beliebig langen Kreisbogen.
Da die Seite c vom Eckpunkt C ausgeht und genauso lang ist wie die Seite a, nehmen Sie die Länge der Seite a in den Zirkel, stechen im Eckpunkt C ein und schlagen einen beliebig langen Kreisbogen ab.
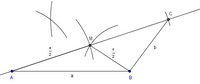
Der Schnittpunkt der beiden Kreisbögen ergibt laut Skizze den Eckpunkt D.
Verbinden Sie diesen mit den beiden anderen Eckpunkten, um das Dreieck (die zweite Hälfte des Parallelogramms) fertigzustellen.
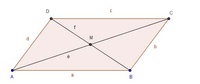
Beschriften Sie zuletzt alle Eckpunkte, Seiten und Winkel des Parallelogramms.
Ziehen Sie die Seiten mit einem weichen Bleistift oder einem Buntstift nach, um das Parallelogramm klar von den Hilfslinien abzuheben.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Iman
Das war eindeutig die beste Erklärung die man überhaupt zusammenstellen kann! Danke ;-)
Christoph
Danke! Ohne euch wäre ich an der Übung sicher noch Stunden gesessen!
Victor
Diese Erklärung war besser als die die mir meine Lehrerin gegeben hat.
Dominik
Danke hat mir sehr weiter geholfen hab morgen einen mathe test
Ahmet
Danke!
Konnte meinem Sohn befinden Hausaufgaben wirklich helfen und er hat es verstanden.
Daumen hoch!