Division durch eine dreistellige Zahl
In diesem Kapitel wollen wir Ihnen erklären, wie Sie eine Zahl durch eine dreistellige Zahl dividieren können.
Die Überschlagsrechnung vor der Durchführung der eigentlichen Division sowie die Probe danach lassen wir in diesem Kapitel unberücksichtigt.
Beispiel:
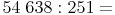
Schritt 1: Stellenwertbestimmung
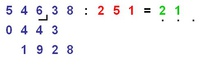
Wir fassen (mit der höchsten Stelle beginnend) so viele Ziffern des Dividenden zusammen, damit diese eine gleich große oder größere Zahl als den Divisor ergeben.
In unserem Fall müssen wir ein Hackerl nach der 6 (Hunderterstelle) machen.
Da wir das Hackerl an der Hunderterstelle gemacht haben, müssen wir nach dem =Zeichen 3 Punkte machen. Für die Stelle an der das Hackerl gemacht wurde und für alle Stellen rechts davon werden nun Punkte gemacht: Unser Ergebnis wird also dreistellig sein.
Schritt 2:
251 ist in 546 genau 2 Mal enthalten.
Die erste Stelle des Ergebnisses ist also eine 2.
2 mal 1 ist 2 - und 4 ist 6: 4 wird unter jener Ziffer mit dem Hackerl geschrieben.
2 mal 5 ist 10 - und 4 sind 14: 4 wird links von der 4 geschrieben - 1 bleibt Rest.
2 mal 2 sind 4 und 1 Rest von vorhin sind 5 - und 0 sind 5: = wird links von der 4 geschrieben.
Schritt 3:
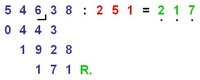
Nächste Stelle 3 herab
Um weiterrechnen zu können, wird die Ziffer des nächstkleineren Stellenwertes (Zehner) an den Rest von vorhin angehängt, was nun die Zahl 443 ergibt.
Schritt 4:
251 ist in 443 genau 1 Mal enthalten.
Die zweite Stelle des Ergebnisses ist also eine 1.
1 mal 1 sind 1 - und 2 sind 3: 2 wird unter der 3 von vorhin geschrieben.
1 mal 5 sind 5 - und 9 sind 14: 9 wird unter der 4 von vorhin geschrieben - 1 bleibt Rest.
1 mal 2 sind 2 und 1 Rest von vorhin sind 3 - und 1 sind 4: 1 wird unter der 4 von oben geschrieben.
Schritt 5:
Nächste Stelle 8 herab
Um weiterrechnen zu können, wird die Ziffer des nächstkleineren Stellenwertes (Einer) an den Rest von vorhin angehängt, was nun die Zahl 1 928 ergibt.
Schritt 6:
251 ist in 1 928 genau 7 Mal enthalten.
Die vierte Stelle des Ergebnisses ist also eine 7.
7 mal 1 ergibt 7 - und 1 ist 8: 1 wird unter der 8 von vorhin geschrieben.
7 mal 5 ergibt 35 - und 7 sind 42: 7 wird unter der 2 von vorhin geschrieben - 4 bleiben Rest.
7 mal 2 ergibt 14 und 4 Rest von vorhin ergeben 18 - und 1 sind 19: 1 wird unter der 9 von vorhin geschrieben.
Das Ergebnis der Division lautet also 217, es bleiben allerdings 171 Rest.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar





owo
geil.