Division durch eine zweistellige Zahl
In diesem Kapitel wollen wir Ihnen erklären, wie Sie eine Zahl durch eine zweistellige Zahl dividieren können.
Die Überschlagsrechnung vor der Durchführung der eigentlichen Division sowie die Probe danach lassen wir in diesem Kapitel unberücksichtigt.
Beispiel:
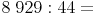
Schritt 1: Stellenwertbestimmung
Wir fassen (mit der höchsten Stelle beginnend) so viele Ziffern des Dividenden zusammen, damit diese eine gleich große oder größere Zahl als den Divisor ergeben.
In unserem Fall müssen wir ein Hackerl nach der 9 (Hunderterstelle) machen.
Da wir das Hackerl an der Hunderterstelle gemacht haben, müssen wir nach dem =Zeichen 3 Punkte machen. Für die Stelle an der das Hackerl gemacht wurde und für alle Stellen rechts davon werden nun Punkte gemacht: Unser Ergebnis wird also dreistellig sein.
Schritt 2:
44 ist in 89 genau 2 Mal enthalten.
Die erste Stelle des Ergebnisses ist also eine 2.
2 mal 4 ist 8 - und 1 ist 9: 1 wird unter jener Ziffer mit dem Hackerl geschrieben. 2 mal 4 ist 8 - und 0 ist 8: 0 wird links von der 1 geschrieben.
Schritt 3:
Nächste Stelle 2 herab
Um weiterrechnen zu können, wird die Ziffer des nächstkleineren Stellenwertes (Zehner) an den Rest von vorhin angehängt, was nun die Zahl 12 ergibt.
Schritt 4:
44 ist in 12 gar nicht (also 0 Mal) enthalten.
Die zweite Stelle des Ergebnisses ist also eine 0.
0 mal 4 sind 0 - und 2 sind 2: 2 wird unter der 2 von vorhin geschrieben. 0 mal 4 sind 0 - und 1 ist 1: 1 wird unter der 1 von vorhin geschrieben.
Schritt 5:
Nächste Stelle 9 herab
Um weiterrechnen zu können, wird die Ziffer des nächstkleineren Stellenwertes (Einer) an den Rest von vorhin angehängt, was nun die Zahl 129 ergibt.
Schritt 6:
44 ist in 129 genau 2 Mal enthalten.
Die vierte Stelle des Ergebnisses ist also eine 2.
2 mal 4 ergibt 8 - und 1 ist 9: 1 wird unter der 9 von vorhin geschrieben. 2 mal 4 ergibt 8 - und 4 sind 12: 4 wird unter der 2 von vorhin geschrieben.
Das Ergebnis der Division lautet also 202, es bleiben allerdings 41 Rest.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar






Lucas
Kurz und knackig :D
Leicht
Leicht
Tati
Danke Danke Danke... Mein/e Mahtheheld/in!!!! : )))..... Endlich, nach 30 Jahren aus der Schule habe ich das zweistellige Dividieren verstanden und kann auch meiner Tochter helfen!!!!! Vielen Dank!!!
Sabine
Danke - jetzt weiß ich es wieder! Sehr gut erklärt!
Meli
Gibt's einen Trick, wie man das schnell im Kopf ausrechnet?
Daris
Hat mir geholfen ☺
Gretl
Erklärung prinzipiell gut, danke; es wäre aber deutlicher, wenn statt 44 zB 43 gewählt würde - jedenfalls nicht idente Ziffern für den 2stelligen Divisor. Dann wird klarer, wie es von rechts nach links geht.
David
sehr cool
Daniel Latikaynen
Kann mich der Vorpostenden Gretl nur anschliessen, der Fall eines aus zwei gleichen Ziffern bestehenden Divisors ist zwar ein gutes Übungsbeispiel weil man extra aufpassen muss wegen der Stellenwerte beim Zurückmultiplizieren, aber gerade für ein schrittweises Erklären wäre es hilfreich das Beispiel auf einen Wert wie 34 oder 43 abzuändern.
Babak Houman
was bedeutet genau im Schritt 2 der Satz: "2 mal 4 ist 8 - und 0 ist 8", ich nehme an, es soll heißen: "2 mal 4 ist 8 und 8 - 8 ist 0"
Rzzz
Hat mir nicht geholfen,
Schönen Dank.
Monika Heitmann
Ist viel einfacher, wenn man die Zwischenergebnisse hinschreibt (wie in Deutschland üblich) - so ist es kompliziert und viel zu fehleranfällig und ich kann leider verstehen, dass meine Tochter Mathe Ka*** findet.
Wenn man sich die Mathematik einfach gestaltet -und das ist sie im Grunde genommen- kann sie Spaß machen und (und das ist der Clou!) die Rechnerei führt zu richtigen Ergebnissen.