Berechnung der Höhe 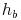 eines Parallelogramms, wenn der Flächeninhalt und die Seite b gegeben sind
eines Parallelogramms, wenn der Flächeninhalt und die Seite b gegeben sind
Beispiel:
Von einem Parallelogramm kennt man die Länge der Seite b = 12 cm. Der Flächeninhalt beträgt 102 cm². Berechnen Sie die Länge der Höhe 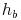 dieses Parallelogramms!
dieses Parallelogramms!
Herleitung der Formel:
Aus dem vorherigen Kapitel wissen wir bereits, dass sich der Flächeninhalt eines Parallelogramms aus dem Produkt einer Seiten und ihrer dazugehörigen Höhe errechnet:
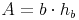
Nachdem wir den Flächeninhalt und die Seite b des Parallelogramms kennen, die Höhe 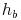 allerdings nicht, formen wir unsere Formel so um, bis die Höhe allein auf einer Seite der Gleichung steht. Dazu dividieren wir beide Seiten der Gleichung durch die Seite b:
allerdings nicht, formen wir unsere Formel so um, bis die Höhe allein auf einer Seite der Gleichung steht. Dazu dividieren wir beide Seiten der Gleichung durch die Seite b: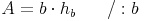
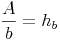
Beispiel (Forts.):
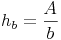
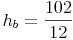
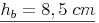
Die Länge der Höhe auf die Seite b des Parallelogramms beträgt 12 cm!
Probe: Wir setzen in die Flächeninhaltsformel ein
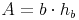
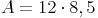
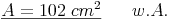
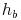 eines Parallelogramms, wenn der Flächeninhalt und die Seite b gegeben sind:
eines Parallelogramms, wenn der Flächeninhalt und die Seite b gegeben sind: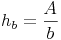
Höhe auf b = Flächeninhalt : Seite b
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar