Bewegungsaufgaben
(2 Fahrzeuge fahren in die gleiche Richtung)
In diesem Kapitel zeigen wir, wie man Bewegungsaufgaben lösen kann, wenn zwei Fahrzeuge in die gleiche Richtung fahren.
Bei der Lösung von Bewegungsaufgaben geht man davon aus, dass:
- die Bewegung gleichförmig verlauft (= konstante Geschwindigkeit vom Ausgangs- bis zum Endpunkt)
- keine Pausen eingelegt werden
- keine Hindernisse auf der Strecke auftreten
Arbeitsblätter mit weiteren Übungsaufgaben finden Sie im Bereich "Arbeitsblätter".
Grundformel
Unter Berücksichtigung der oben genannten Bedingungen berechnet man die Wegstrecke s in Abhängigkeit der Geschwindigkeit v und der Zeit t mit folgender Formel:
Weg = Geschwindigkeit mal Zeit
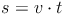
Beispiel
Kurt fährt mit seinem Fahrrad um 9 Uhr mit einer durchschnittlichen Geschwindigkeit von 18 km/h in Richtung Kleindorf. Sein Bruder Klaus bricht 18 Minuten später auf und fährt ihm mit einer Geschwindigkeit von 24 km/h nach.
Wann holt Klaus seinen Bruder Kurt ein und wie weit ist jeder Radfahrer gefahren?
1. Erstellen einer Tabelle
Beide Personen (Kurt, Klaus) bekommen eine eigene Zeile; Geschwindigkeit, Zeit, Weg eine eigene Spalte.
| Person | Geschwindigkeit (v) | Zeit (t) | Weg (s = v . t) |
|---|---|---|---|
| Kurt | |||
| Klaus |
2. Vervollständigen der Tabelle
In die Spalte Geschwindigkeit werden die beiden Geschwindigkeiten in km/h geschrieben, mit denen die beiden Brüder unterwegs sind.
Die Zeit, die Kurt benötigt, ist unbekannt - somit wird hier die Variable x angeschrieben. Die Zeit, die Klaus benötigt, ist ebenso unbekannt. Allerdings wissen wir, dass Klaus um 18 Minuten später wegfährt, somit müsste in dieses Feld der Wert x - 18 geschrieben werden.
Allerdings ist die Geschwindigkeit in Kilometer pro Stunde (km/h) angegeben. Daher muss auch die Zeit in Stunden angegeben werden: x - 0,3
Umrechnung:
18 Minuten = 18 : 60 = 0,3 Stunden
| Person | Geschwindigkeit (v) | Zeit (t) | Weg (s = v . t) |
|---|---|---|---|
| Kurt | 18 km/h | x | 18 . x |
| Klaus | 24 km/h | x - 0.3 | 24 . (x - 0.3) |
3. Aufstellen der Gleichung
Die beiden in der Tabelle berechneten Wege werden nun zu einer Gleichung gesetzt.
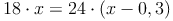
4. Lösen der Gleichung
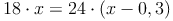
Zuerst wird die Klammer ausmultipliziert: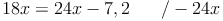
Durch Äquivalenzumformungen wird nun x allein auf eine Seite gebracht: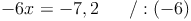
Abschließend noch durch -6 dividieren, um x allein auf einer Seite stehen zu haben:
5. Lösung
Aus unserer Tabelle wisen wir, dass Kurt x Stunden gefahren ist. Kurt ist um 9 Uhr weggefahren, fährt 1,2 Stunden und trifft somit seinen Bruder um 10:12 Uhr.
Anmerkung:
0,2 Stunden = 0,2 . 60 = 12 Minuten
9 Uhr + 1 Stunde und 12 inuten = 10:12 Uhr
Um den zurückgelegten Weg zum Zeitpunkt x zu ermitteln, sehen wir wieder in die Tabelle:
18 . x = 18 . 1,2 = 21,6 km
6. Antwort
Klaus holt seinen Bruder Kurt um 10:16 Uhr ein. Zu diesem Zeitpunkt sind die beiden jeweils 21,6 km gefahren.
Bei der Lösung von Bewegungsaufgaben geht man davon aus, dass:
- die Bewegung gleichförmig verlauft (= konstante Geschwindigkeit)
- keine Pausen eingelegt werden
- keine Hindernisse auf der Strecke auftreten
Zum Lösen solcher Bewegungsaufgaben, bietet es sich an, eine Tabelle und daraus dann eine Gleichung zu erstellen.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
