Mischungsaufgaben mit Prozentangaben
Bei Mischungsaufgaben werden mehrere Stoffe mit unterschiedlichen Eigenschaften (Preis, Alkoholgehalt, ...) gemischt, um einen Stoff mit neuen Eigenschaften zu erhalten.
In diesem Kapitel zeigen wir Ihnen ein Musterbeispiel, wie Sie solche Aufgaben mit Prozentangaben lösen können.
Arbeitsblätter mit weiteren Übungsaufgaben finden Sie im Bereich "Arbeitsblätter".
Beispiel:
3 Liter 40 %iger Alkohol und 5 Liter 20 %iger Alkohol sollen vermischt werden. Wie hoch ist der %-Gehalt der neu entstandenen Mischung?
1. Erstellen einer Tabelle
Jede Flüssigkeit (40 %iger Alkohol, 20 %iger Alkohol, Mischung) bekommt eine eigene Zeile. Sorte, Menge, %-Gehalt und Menge mal %-Gehalt eine eigene Spalte.
| Sorte | Menge | %-Gehalt | Menge mal Prozentgehalt |
|---|---|---|---|
| 40 %iger Alkohol | 3 Liter | 40 % | |
| 20 %iger Alkohol | 5 Liter | 20% | |
| Mischung |
2. Vervollständigen der Tabelle
%-Gehalt: Nachdem Prozent Hundertstel bedeutet, wandeln wir die %-Werte in Dezimalzahlen um: 1% = 1/100 = 0,01! Eine genaue Anleitung dazu finden Sie im Kapitel "Brüche".
Somit sind 40% = 40/100 = 0,40 und 20% = 20/100 = 0,20.
Menge mal Prozentgehalt: Wie der Titel dieser Spalte schon verrät, wird hier die Menge mit dem Prozentgehalt multipliziert.
Mischung: Mischt man 3 Liter mit 5 Liter zusammen, so erhält man 3 + 5 = 8 Liter für die Menge. Den Prozentgehalt der Mischung kennen wir nicht, daher schreiben wir hier die Variable x an.
| Sorte | Menge | %-Gehalt | Menge mal Prozentgehalt |
|---|---|---|---|
| 40 %iger Alkohol | 3 Liter | 40 % = 0.40 | 3 . 0.40 |
| 20 %iger Alkohol | 5 Liter | 20 % = 0.20 | 5 . 0.20 |
| Mischung | 8 Liter | x | 8 . x |
3. Aufstellen der Gleichung
Menge mal Prozentgehalt des 40 %ien Alkohols und Menge mal Prozentgehalt des 20 %igen Alkohols zusammen ergeben Menge mal Prozentgehalt der Mischung.
Als Gleichung wird dies folgendermaßen aufgeschrieben:
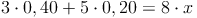
4. Lösen der Gleichung
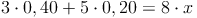
Zuerst wird multipliziert: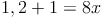
Nun können die beiden Werte der linken Seite unserer Gleichung addiert werden: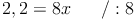
Abschließend noch durch 8 dividieren, um x allein auf einer Seite stehen zu haben: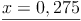
5. Lösung:
Nun wandeln wir diese Dezimalzahl wieder in die Prozentschreibweise um. Dazu multiplizieren wir mit 100: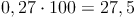
6. Antwort:
Man erhält 8 Liter 27,5 %igen Alkohols.
Bei Mischungsaufgaben werden mehrere Stoffe mit unterschiedlichen Eigenschaften (Preis, Alkoholgehalt, ...) gemischt, um einen Stoff mit neuen Eigenschaften zu erhalten.
Dazu bietet es sich an, eine Tabelle und daraus dann eine Gleichung zu erstellen.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
