Textgleichungen: Quadrat und Rechteck (mit zwei gleichen Größen)
Beispiel:
Verlängert man eine Seite eines Quadrats um 4 cm und verkürzt die andere Seite um 6 cm, so erhält man ein Rechteck mit gleichem Flächeninhalt.
Berechnen Sie die Länge der Seite dieses Quadrats!
Als Unbekannte (Variable) verwenden wir in diesem Beispiel den Buchstaben x!
Seite mal Seite
1) Quadrat:
Länge: 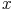
Breite: 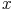
Flächeninhalt: 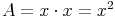
2) Rechteck:
Länge: 
Breite: 
Flächeninhalt: 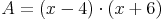
3) Aufstellen der Gleichung:
Da die beiden Flächeninhalte des Quadrats und des Rechtecks gleich groß sind, kann man sie mit einem =Zeichen miteinander vergleichen: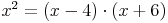
4) Lösen der Gleichung:
Ausmultiplizieren der Klammern: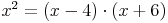
Zusammenfassen gleicher Variablen: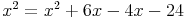
x² kommt auf beiden Seiten der Gleichung vor, kann also weglassen werden:
Wir bringen 24 auf die andere Seite der Gleichung: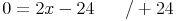
Abschließend muss noch durch 2 dividiert werden: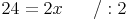
Endergebnis: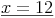
5) Antwort:
Die Länge der Seite des Quadrats beträgt 12cm.
Sind 2 Größen gleich, so ist das Aufstellen einer Gleichung recht einfach. Die beiden Größen können einfach miteinander verglichen werden.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar