a - b - Beta

Konstruktion eines Deltoids, wenn die Seite a, die Seite b und der Winkel Beta gegeben sind

Konstruktion eines Deltoids, wenn die Seite a, die Seite b und der Winkel Beta gegeben sind

geg.: Deltoid:

\begin{align} & a = 3\ cm \\ & b = 6\ cm \\ & \beta = 130^\circ \\ \end{align}

ges.: Konstruktion

Schritt 1: Skizze

Zeichnen Sie zuerst eine Skizze des Deltoids und beschriften Sie diese vollständig (Seiten, Eckpunkte, Winkel).

Die gegebenen Bestimmungsstücke werden nun färbig markiert, um nachher die Konstruktion einfacher durchführen zu können.

Schritt 2: Konstruktion des Eckpunktes A

Beginnen Sie mit der Konstruktion des Eckpunktes B und zeichnen sie zugleich eine Hilfsgerade, auf der später die Seite a liegen soll.

Legen sie diese Hilfsgerade idealerweise gleich so, wie die Seite a später auch in etwa liegen könnte.

Schritt 3: Konstruktion des Winkels 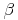\beta

In der Skizze können wir erkennen, dass der Winkel 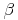\beta im Eckpunkt B zwischen den Seiten a und b liegt.

Konstruieren Sie deshalb im Eckpunkt B den Winkel 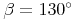\beta = 130^\circ

Schritt 4: Konstruktion der Seite a

In der Skizze können wir erkennen, dass die Seiten a vom Eckpunkt B aus geht und auf dem nach oben liegenden Winkelschenkel des Winkels 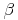\beta liegt.

Nehmen Sie daher die Länge der Seite a = 3 cm in den Zirkel, stechen Sie im Eckpunkt B ein und schlagen Sie diesen Wert auf dem oberen Winkelschenkel ab.

Dadurch entsteht nun der Eckpunkt A des Deltoids.

Schritt 5: Konstruktion der Seite b

In der Skizze können wir erkennen, dass die Seiten b vom Eckpunkt B aus geht und auf dem nach unten liegenden Winkelschenkel des Winkels 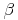\beta liegt.

Nehmen Sie daher die Länge der Seite b = 6 cm in den Zirkel, stechen Sie im Eckpunkt B ein und schlagen Sie diesen Wert auf dem unteren Winkelschenkel ab.

Dadurch entsteht nun der Eckpunkt C des Deltoids.

Schritt 6: Konstruktion der Seite c

Da die Seite c genauso lang ist wie die Seite a und das Deltoid bezüglich der Diagonale AC eine symmetrische Figur ist, können wir nun die Konstruktionsschritte von vorhin auch auf der rechten Seite anwenden.

Nehmen Sie daher die Länge der Seite c = 3 cm in den Zirkel, stechen Sie im Eckpunkt A ein und schlagen Sie diesen Wert nach rechts unten ab.

Schritt 7: Konstruktion der Seite d

Wir wissen bereits, dass die Seiten b und d eine Deltoids gleich lang sind.

Nun nehmen Sie die Länge der Seite d = 6 cm in den Zirkel, stechen im Eckpunkt C ein und schlagen diesen Wert nach oben ab.

Dort wo sich die beiden Kreisbögen schneiden, befindet sich der Eckpunkt D des Deltoids.

Schritt 8: Verbinden und Beschriftung

Verbinden Sie die Eckpunkte A, B, C und D nun der Reihe nach.

Beschriften Sie zuletzt alle fehlenden Eckpunkte, Seiten und Winkel des Deltoids.

Ziehen Sie die Seiten mit einem weichen Bleistift oder einem Buntstift nach, um das Deltoid klar von den Hilfslinien abzuheben.

Kommentar #456 von TheChrisxxx22 29.08.11 08:39
TheChrisxxx22

da oben steht "...der Winkel Beta gegeben sind" ,aber darunter steht:
alpha = 130°
Es müsste beta= 130° heißen!!

Kommentar #460 von Admin 29.08.11 08:40
Admin

Vielen Dank für die Info!
Der Fehler wurde soeben behoben!
lg

Kommentar #43894 von lola 26.04.20 15:45
lola

Hallo?Wie ist es mit der Hielfslinie gemeint.mit um antworten.danke lg

Kommentar #45284 von Anonym 18.02.21 12:00
Anonym

Danke denn ich habe das was die Lehrerin gesagt hat nicht verstanden hat mir sehr geholfen

Kommentar verfassen