a - b - e

Konstruktion eines Deltoids, wenn die Seite a, die Seite b und die Diagonale e gegeben sind

geg.: Deltoid:

$\begin{align} & a = 4\ cm \\ & b = 6\ cm \\ & e = 8\ cm \\ \end{align}$

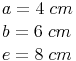
ges.: Konstruktion

Schritt 1: Skizze

Zeichnen Sie zuerst eine Skizze des Deltoids und beschriften Sie diese vollständig (Seiten, Eckpunkte, Winkel).

Die gegebenen Bestimmungsstücke werden nun färbig markiert, um nachher die Konstruktion einfacher durchführen zu können.

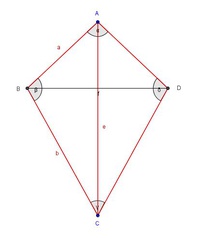
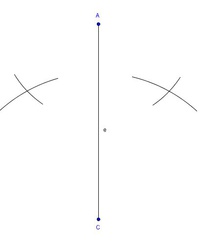
Schritt 2: Konstruktion der Diagonale e

Beginnen Sie mit der Konstruktion der Diagonale e = 8 cm, welche die Eckpunkte A und C miteinander verbindet.

Beschriften Sie die gezeichnete Diagonale und die beiden Eckpunkte.

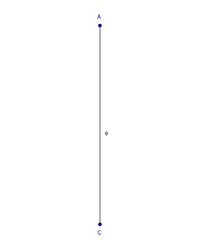
Schritt 3: Konstruktion der Seite(n) b

In der Skizze können wir erkennen, dass die Seiten b vom Eckpunkt C aus gehen.

Nehmen Sie daher die Länge der Seite b = 6 cm in den Zirkel, stechen Sie im Eckpunkt C ein und schlagen Sie auf beiden Seiten der Diagonale e ab.

Schritt 4: Konstruktion der Seite(n) a

In der Skizze können wir erkennen, dass die Seiten a vom Eckpunkt A aus gehen.

Nehmen Sie daher die Länge der Seite a = 4 cm in den Zirkel, stechen Sie im Eckpunkt A ein und schlagen Sie auf beiden Seiten der Diagonale e ab.

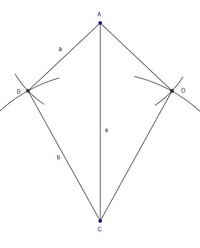
Schritt 5: Verbinden der Eckpunkte

Dort wo sich jeweils die beiden Kreisbögen schneiden, befinden sich die Eckpunkte B (links der Diagonale e) und D (rechts der Diagonale e).

Markieren und beschriften Sie nun diese beiden Eckpunkte und verbinden Sie anschließend die Eckpunkte A, B, C und D der Reihe nach.

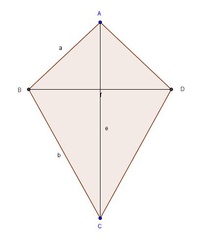
Schritt 6: Beschriftung

Beschriften Sie zuletzt alle fehlenden Eckpunkte, Seiten und Winkel des Deltoids.

Ziehen Sie die Seiten mit einem weichen Bleistift oder einem Buntstift nach, um das Deltoid klar von den Hilfslinien abzuheben.

Kommentar #334 von maria 12.01.11 17:01 maria: meine längen waren
f=5 cm diagonale
a=3cm
b=4 cm
ich weis jetzt nicht ob es richtig ausschaut ????
Kommentar #7718 von philip 30.05.13 11:51 philip: Aber für a b f gibt es ja ein eigenes Thema
Kommentar #43828 von Tobi 15.04.20 09:07 Tobi: Jep, für a b f gibt es eine eigene Erklärung. Aber wirklich ne tolle Website. Habe jetzt ne 1 in Mathe. :)
Kommentar #44804 von Bimou 29.11.20 11:16 Bimou: Vielen Dank, meine Hausaufgaben sind gerettet!

Lg
Kommentar #46646 von Amelie 13.12.21 22:31 Amelie: Was ist wenn ich die Diagonale e hab, die Seite a und den Winkel betta also ß
Kommentar #48584 von Olive 16.05.24 19:34 Olive: Einfach beste Website!!! Ohne hätte ich die Mathe-Hausaufgaben nicht geschafft!!!!!
Empfehle ich weiter!!!!!